剑指Offer
链表
JZ35 复杂链表的复制
复杂链表的复制_牛客题霸_牛客网 (nowcoder.com)
描述
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针random指向一个随机节点),请对此链表进行深拷贝,并返回拷贝后的头结点。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)。 下图是一个含有5个结点的复杂链表。图中实线箭头表示next指针,虚线箭头表示random指针。为简单起见,指向null的指针没有画出。

示例:
输入:{1,2,3,4,5,3,5,#,2,#}
输出:{1,2,3,4,5,3,5,#,2,#}
解析:我们将链表分为两段,前半部分{1,2,3,4,5}为ListNode,后半部分{3,5,#,2,#}是随机指针域表示。
以上示例前半部分可以表示链表为的ListNode:1->2->3->4->5
后半部分,3,5,#,2,#分别的表示为
1的位置指向3,2的位置指向5,3的位置指向null,4的位置指向2,5的位置指向null
如下图:

示例1
输入:
{1,2,3,4,5,3,5,#,2,#}
返回值:
{1,2,3,4,5,3,5,#,2,#}
题解:
unordered_map可以解:但空间复杂度O(n)
O(1)的解法:
关键点就是

实现从上者到下者的变换,然后再分离两个链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution {
public:
RandomListNode* Clone(RandomListNode* pHead) {
if (pHead == nullptr)
return nullptr;
RandomListNode *next = nullptr;
RandomListNode *cur = pHead;
while (cur != nullptr) {
RandomListNode *copyNode = new RandomListNode(cur->label);
next = cur->next;
cur->next = copyNode;
copyNode->next = next;
cur = next;
}
RandomListNode *copyCur = nullptr;
cur = pHead;
while (cur != nullptr) {
next = cur->next->next;
copyCur = cur->next;
copyCur->random = (cur->random == nullptr ? nullptr : cur->random->next);
cur = next;
}
cur = pHead;
RandomListNode *res = cur->next;
while (cur != nullptr) {
next = cur->next->next;
copyCur = cur->next;
cur->next = next;
copyCur->next = (next == nullptr ? nullptr : next->next);
cur = next;
}
return res;
}
};
|
刚写出来的程序有一个大问题,值得留意

树
JZ55 二叉树的深度
二叉树的深度_牛客题霸_牛客网 (nowcoder.com)
描述
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度,根节点的深度视为 1 。
数据范围:节点的数量满足 0≤n≤100 ,节点上的值满足 0≤val≤100
进阶:空间复杂度 O*(1) ,时间复杂度O*(n)
假如输入的用例为{1,2,3,4,5,#,6,#,#,7},那么如下图:

示例1
输入:
{1,2,3,4,5,#,6,#,#,7}
返回值:
4
复制
示例2
输入:
{}
返回值:
0
题解:
递归遍历,没啥好说的
1
2
3
4
5
6
7
8
|
class Solution {
public:
int TreeDepth(TreeNode* pRoot) {
if (pRoot == nullptr)
return 0;
return max(TreeDepth(pRoot->left), TreeDepth(pRoot->right)) + 1;
}
};
|
JZ54 二叉搜索树的第K个结点
二叉搜索树的第k个节点_牛客题霸_牛客网 (nowcoder.com)
描述
给定一棵结点数为n 二叉搜索树,请找出其中的第 k 小的TreeNode结点值。
1.返回第k小的节点值即可
2.不能查找的情况,如二叉树为空,则返回-1,或者k大于n等等,也返回-1
3.保证n个节点的值不一样
数据范围: 0≤n≤1000,0≤k≤1000,树上每个结点的值满足0≤val≤1000
如输入{5,3,7,2,4,6,8},3时,二叉树{5,3,7,2,4,6,8}如下图所示:

该二叉树所有节点按结点值升序排列后可得[2,3,4,5,6,7,8],所以第3个结点的结点值为4,故返回对应结点值为4的结点即可。
示例1
输入:
{5,3,7,2,4,6,8},3
复制
返回值:
4
复制
示例2
输入:
{},1
复制
返回值:
-1
题解:
中序递归遍历,关于二叉树的非递归遍历也得练练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param proot TreeNode类
* @param k int整型
* @return int整型
*/
int KthNode(TreeNode* proot, int k) {
// write code here
if (proot == nullptr || k < 1)
return -1;
int count = 0;
TreeNode *res = nullptr;
midOrder(proot, res, count, k);
if (res == nullptr)
return -1;
else
return res->val;
}
void midOrder(TreeNode *root, TreeNode *&res, int &count, int k) {
if (count > k || root == nullptr)
return;
midOrder(root->left, res, count, k);
count++;
if (count == k){
res = root;
return;
}
midOrder(root->right, res, count, k);
}
};
|
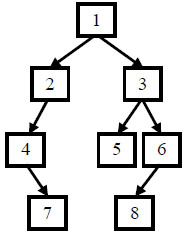
JZ7 重建二叉树
重建二叉树_牛客题霸_牛客网 (nowcoder.com)
描述:
给定节点数为 n 的二叉树的前序遍历和中序遍历结果,请重建出该二叉树并返回它的头结点。
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建出如下图所示。
提示:
1.vin.length == pre.length
2.pre 和 vin 均无重复元素
3.vin出现的元素均出现在 pre里
4.只需要返回根结点,系统会自动输出整颗树做答案对比
示例1
输入:
[1,2,4,7,3,5,6,8],[4,7,2,1,5,3,8,6]
返回值:
{1,2,3,4,#,5,6,#,7,#,#,8}
说明:
返回根节点,系统会输出整颗二叉树对比结果,重建结果如题面图示
示例2
输入:
[1],[1]
返回值:
{1}
示例3
输入:
[1,2,3,4,5,6,7],[3,2,4,1,6,5,7]
返回值:
{1,2,5,3,4,6,7}
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param preOrder int整型vector
* @param vinOrder int整型vector
* @return TreeNode类
*/
TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {
// write code here
if (preOrder.size() == 0 || vinOrder.size() == 0)
return nullptr;
int p = 0, v = 0;
for (int i = 0; i < vinOrder.size(); i++) {
if (vinOrder[i] == preOrder[p]){
v = i;
break;
}
}
TreeNode *root = new TreeNode(preOrder[0]);
vector<int> leftPre(preOrder.begin() + 1, preOrder.begin() + 1 + v);
vector<int> leftVin(vinOrder.begin(), vinOrder.begin() + v);
root->left = reConstructBinaryTree(leftPre, leftVin);
vector<int> rightPre(preOrder.begin() + 1 + v, preOrder.end());
vector<int> rightVin(vinOrder.begin() + 1 + v, vinOrder.end());
root->right = reConstructBinaryTree(rightPre, rightVin);
return root;
}
};
|
JZ26 树的子结构
树的子结构_牛客题霸_牛客网 (nowcoder.com)
描述
输入两棵二叉树A,B,判断B是不是A的子结构。(我们约定空树不是任意一个树的子结构)
假如给定A为{8,8,7,9,2,#,#,#,#,4,7},B为{8,9,2},2个树的结构如下,可以看出B是A的子结构

数据范围:
0 <= A的节点个数 <= 10000
0 <= B的节点个数 <= 10000
示例1
输入:
{8,8,7,9,2,#,#,#,#,4,7},{8,9,2}
返回值:
true
示例2
输入:
{1,2,3,4,5},{2,4}
返回值:
true
示例3
输入:
{1,2,3},{3,1}
返回值:
false
题解:
挺好玩的,如果两个之一节点是空的直接返回false,如果不是则递归寻找结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
//主函数,如果两个都是空则直接false
bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2) {
if (pRoot1 == nullptr || pRoot2 == nullptr)
return false;
return subTree(pRoot1, pRoot2) || //看看对于当前节点是不是这个结构
HasSubtree(pRoot1->left, pRoot2) || //看看左子树有没有
HasSubtree(pRoot1->right, pRoot2); //看看右子树有没有
}
bool subTree(TreeNode *pRoot1, TreeNode *pRoot2) {
//基本情况
if (!pRoot1 && pRoot2) //第一棵树先走完了,说明这里没有
return false;
if ( !pRoot2) //只要第二颗树走完则一定有
return true;
//当前值相等,并且要左右子树都一样
return (pRoot1->val == pRoot2->val) &&
subTree(pRoot1->left, pRoot2->left) &&
subTree(pRoot1->right, pRoot2->right);
}
};
|
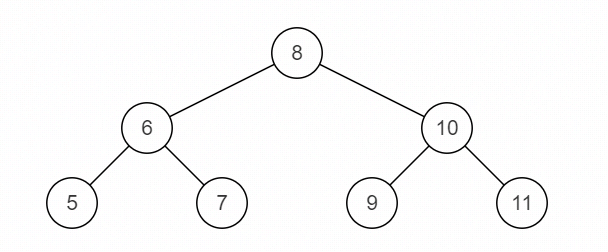
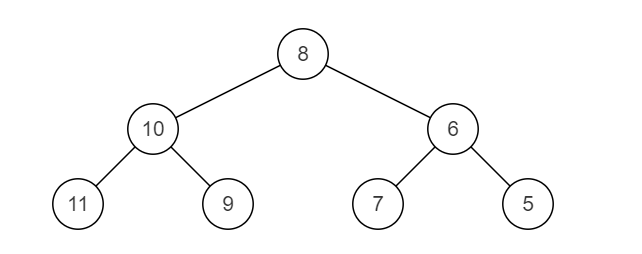
JZ27 二叉树的镜像
二叉树的镜像_牛客题霸_牛客网 (nowcoder.com)
描述
操作给定的二叉树,将其变换为源二叉树的镜像。
数据范围:二叉树的节点数 0≤n≤1000 , 二叉树每个节点的值 0≤val≤1000
要求: 空间复杂度 O*(n) 。本题也有原地操作,即空间复杂度O*(1) 的解法,时间复杂度 O*(*n)
比如:
源二叉树
镜像二叉树
示例1
输入:
{8,6,10,5,7,9,11}
复制
返回值:
{8,10,6,11,9,7,5}
复制
说明:
如题面所示
示例2
输入:
{}
复制
返回值:
{}
题解:
递归调用即可,退出条件为当前节点为空,获取当前节点左右子树并交换
1
2
3
4
5
6
7
8
9
10
11
12
13
|
TreeNode* Mirror(TreeNode* pRoot) {
// write code here
//退出条件
if (!pRoot)
return nullptr;
//获取左右子树
TreeNode *leftMi = Mirror(pRoot->left);
TreeNode *rightMi = Mirror(pRoot->right);
//交换
pRoot->left = rightMi;
pRoot->right = leftMi;
return pRoot;
}
|
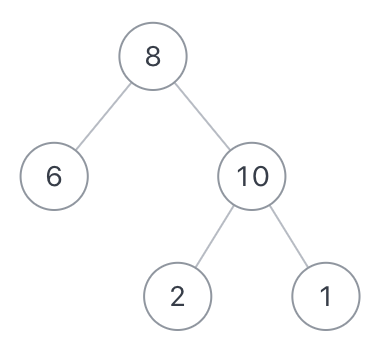
JZ32 从上往下打印二叉树
从上往下打印二叉树_牛客题霸_牛客网 (nowcoder.com)
描述
不分行从上往下打印出二叉树的每个节点,同层节点从左至右打印。例如输入{8,6,10,#,#,2,1},如以下图中的示例二叉树,则依次打印8,6,10,2,1(空节点不打印,跳过),请你将打印的结果存放到一个数组里面,返回。
数据范围:
0<=节点总数<=1000
-1000<=节点值<=1000
示例1
输入:
{8,6,10,#,#,2,1}
返回值:
[8,6,10,2,1]
示例2
输入:
{5,4,#,3,#,2,#,1}
返回值:
[5,4,3,2,1]
题解:
很简单的一道题,层序遍历即可(用到队列),首先将根节点入队,后续队列非空情况下弹出一个节点,并同时将该节点左右孩子入队
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
vector<int> PrintFromTopToBottom(TreeNode* root) {
vector<int> res;
if (!root)
return res;
queue<TreeNode *> levelOrder;
TreeNode *cur = root;
levelOrder.push(cur);
while (!levelOrder.empty()) {
TreeNode *temp = levelOrder.front();
levelOrder.pop();
res.push_back(temp->val);
if (temp->left) levelOrder.push(temp->left);
if (temp->right) levelOrder.push(temp->right);
}
return res;
}
};
|
JZ33 二叉搜索树的后序遍历序列
二叉搜索树的后序遍历序列_牛客题霸_牛客网 (nowcoder.com)
描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回 true ,否则返回 false 。假设输入的数组的任意两个数字都互不相同。
数据范围: 节点数量 0≤n≤1000 ,节点上的值满足 1≤val≤105 ,保证节点上的值各不相同
提示:
1.二叉搜索树是指父亲节点大于左子树中的全部节点,但是小于右子树中的全部节点的树。
2.该题我们约定空树不是二叉搜索树
3.后序遍历是指按照 “左子树-右子树-根节点” 的顺序遍历
4.参考下面的二叉搜索树,示例 1
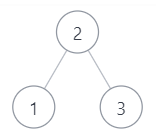
示例1
输入:
[1,3,2]
返回值:
true
说明:
是上图的后序遍历 ,返回true
示例2
输入:
[3,1,2]
返回值:
false
说明:
不属于上图的后序遍历,从另外的二叉搜索树也不能后序遍历出该序列 ,因为最后的2一定是根节点,前面一定是孩子节点,可能是左孩子,右孩子,根节点,也可能是全左孩子,根节点,也可能是全右孩子,根节点,但是[3,1,2]的组合都不能满足这些情况,故返回false
示例3
输入:
[5,7,6,9,11,10,8]
返回值:
true
题解:
考察对中序遍历和后序遍历的理解:可以这么转化思虑,二叉树的非递归都可以使用压栈出栈顺序来实现,我们能对一个vector做的操作有排序,而排序结果正好就是二叉搜索树的中序遍历结果,所以可以采用这种思虑,排序一个数组,将排序后的按照压栈出栈来操作,看最后是否一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public:
bool VerifySquenceOfBST(vector<int> sequence) {
auto len = sequence.size();
if (len == 0)
return false;
vector<int> vinOrder(sequence);
sort(vinOrder.begin(), vinOrder.end()) ;
return isPopOrder(vinOrder, sequence);
}
bool isPopOrder(vector<int> &pushV, vector<int> &popV) {
stack<int> st;
int n = pushV.size();
int i = 0, j = 0;
while (i < n) {
st.push(pushV[i]);
while (!st.empty() && st.top() == popV[j]) {
st.pop();
j++;
}
i++;
}
return i == j;
}
};
|
算法101
BM11 链表相加(二)
链表相加(二)_牛客题霸_牛客网 (nowcoder.com)
描述
假设链表中每一个节点的值都在 0 - 9 之间,那么链表整体就可以代表一个整数。
给定两个这种链表,请生成代表两个整数相加值的结果链表。
例如:链表 1 为 9->3->7,链表 2 为 6->3,最后生成新的结果链表为 1->0->0->0。

示例1
输入:
[9,3,7],[6,3]
返回值:
{1,0,0,0}
说明:
如题面解释
示例2
输入:
[0],[6,3]
返回值:
{6,3}
题解:
反转链表+链表相加(力扣刚刷)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
ListNode *reverseList(ListNode *node) {
ListNode *pre = nullptr;
ListNode *cur = node;
while (cur) {
ListNode *temp = cur->next;
cur->next = pre;
pre = cur;
cur = temp;
}
return pre;
}
ListNode* addInList(ListNode* head1, ListNode* head2) {
// write code here
if (head1 == nullptr)
return head2;
if (head2 == nullptr)
return head1;
head1 = reverseList(head1);
head2 = reverseList(head2);
ListNode *pre = new ListNode(0);
ListNode *cur = pre;
int carry = 0;
while (head1|| head2) {
int val1 = head1 == nullptr?0:head1->val;
int val2 = head2 == nullptr?0:head2->val;
int temp = val1 + val2 + carry;
carry = temp/10;
temp %= 10;
cur->next = new ListNode(temp);
cur = cur->next;
if (head1)
head1 = head1->next;
if (head2)
head2 = head2->next;
}
if (carry)
cur->next = new ListNode(carry);
return reverseList(pre->next);
}
|
::好好刷刷翻转链表的题,这道题边吵边刷都做了一个小时,还是不够熟啊😅😅😅
BM12 单链表的排序
单链表的排序_牛客题霸_牛客网 (nowcoder.com)
描述
给定一个节点数为n的无序单链表,对其按升序排序。
示例1
输入:
[1,3,2,4,5]
返回值:
{1,2,3,4,5}
示例2
输入:
[-1,0,-2]
返回值:
{-2,-1,0}
题解:
把链表转换成数组,然后快排(当然也可以直接在链表上用归并,后面再刷一次)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类 the head node
* @return ListNode类
*/
ListNode* sortInList(ListNode* head) {
// write code here
if (head == nullptr)
return head;
vector<int> val;
while (head) {
val.push_back(head->val);
head = head->next;
}
quickSort(val, 0, val.size() - 1);
ListNode *resHead = new ListNode(0);
ListNode *cur = resHead;
for (int i = 0; i < val.size(); i++) {
cur->next = new ListNode(val[i]);
cur = cur->next;
}
return resHead->next;
}
void quickSort(vector<int> &nums, int l, int r) {
if (l < r) {
int index = l + rand() % (r - l + 1);
swap(nums[index], nums[r]);
vector<int> p = partition(nums, l, r);
quickSort(nums, l, p[0] - 1);
quickSort(nums, p[1] + 1, r);
}
}
vector<int> partition(vector<int> &nums, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (nums[l] < nums[r])
swap(nums[++less], nums[l++]);
else if (nums[l] > nums[r])
swap(nums[l], nums[--more]);
else
++l;
}
swap(nums[r], nums[more]);
vector<int> p = {less + 1, more};
return p;
}
};
|
BM5 合并K个已排序的链表
合并k个已排序的链表_牛客题霸_牛客网 (nowcoder.com)
描述
合并 k 个升序的链表并将结果作为一个升序的链表返回其头节点。
示例1
输入:
[{1,2,3},{4,5,6,7}]
返回值:
{1,2,3,4,5,6,7}
示例2
输入:
[{1,2},{1,4,5},{6}]
返回值:
{1,1,2,4,5,6}
题解:
归并排序思想,需要好好看看,其实就是归并改了一点,如果是数组归并好说,这个是对多个链表归并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
ListNode* mergeKLists(vector<ListNode*>& lists) {
// write code here
if (lists.size() == 0)
return nullptr;
return mergeSort(lists, 0, lists.size() - 1);
}
ListNode *mergeSort(vector<ListNode*> &nodes, int l, int r) {
if (l > r)
return nullptr;
if (l == r)
return nodes[l];
int mid = l +((r - l) >>2);
return merge(mergeSort(nodes, l, mid), mergeSort(nodes, mid + 1, r));
}
ListNode *merge(ListNode *node1, ListNode *node2){
if (!node1)
return node2;
if (!node2)
return node1;
ListNode *pre = new ListNode(0);
ListNode *cur = pre;
while (node1 && node2) {
if (node1->val > node2->val) {
cur->next = node2;
node2 = node2->next;
}
else {
cur->next = node1;
node1 = node1->next;
}
cur = cur->next;
}
if (node1)
cur->next = node1;
if (node2)
cur->next = node2;
return pre->next;
}
|
BM13 判断一个链表是否为回文结构
判断一个链表是否为回文结构_牛客题霸_牛客网 (nowcoder.com)
描述
给定一个链表,请判断该链表是否为回文结构。
回文是指该字符串正序逆序完全一致。
示例1
输入:
{1}
返回值:
true
示例2
输入:
{2,1}
返回值:
false
说明:
2->1
示例3
输入:
{1,2,2,1}
返回值:
true
说明:
1->2->2->1
题解:
一开始想用双指针,结果没解出来,想的复杂了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
bool isPail(ListNode* head) {
// write code here
if (head == nullptr)
return true;
ListNode *fast = head, *slow = head;
while (fast && fast->next) {
fast = fast->next->next;
slow = slow->next;
}
slow = reverse(slow);
fast = head;
while (slow != nullptr) {
if (fast->val != slow->val)
return false;
fast = fast->next;
slow = slow->next;
}
return true;
}
ListNode *reverse(ListNode *node) {
ListNode *pre = nullptr;
ListNode *p = node;
while (p) {
ListNode *next = p->next;
p->next = pre;
pre = p;
p = next;
}
return pre;
}
|
BM14 链表的奇偶重排
链表的奇偶重排_牛客题霸_牛客网 (nowcoder.com)
题解:
第一版,没有断掉原来链表之间的连接,导致出现了环😵😵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
ListNode* oddEvenList(ListNode* head) {
// write code here
if (!head)
return nullptr;
int count = 0;
ListNode *cur = head;
ListNode *odd = new ListNode(0);
ListNode *newHead = odd;
ListNode *even = new ListNode(0);
ListNode *evenh = even;
while (cur) {
count++;
if (count & 1) {
odd->next = cur;
odd = odd->next;
}
else {
even->next = cur;
even = even->next;
}
cur = cur->next;
}
odd->next = evenh->next;
return newHead->next;
}
|
第二版,双指针,奇偶分开
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
ListNode* oddEvenList(ListNode* head) {
// write code here
if (head == nullptr)
return nullptr;
ListNode *odd = head;
ListNode *even = head->next;
ListNode *evenHead = even;
while (even != nullptr && even->next != nullptr) {
odd->next = even->next;
odd = odd->next;
even->next = odd->next;
even = even->next;
}
odd->next = evenHead;
return head;
}
|
BM15 删除有序链表中重复的元素
删除有序链表中重复的元素-I_牛客题霸_牛客网 (nowcoder.com)
描述
删除给出链表中的重复元素(链表中元素从小到大有序),使链表中的所有元素都只出现一次
例如:
给出的链表为1→1→21→1→2,返回1→21→2.
给出的链表为1→1→2→3→31→1→2→3→3,返回1→2→31→2→3.
示例1
输入:
{1,1,2}
返回值:
{1,2}
示例2
输入:
{}
返回值:
{}
题解:
秒了
1
2
3
4
5
6
7
8
9
10
|
ListNode* deleteDuplicates(ListNode* head) {
// write code here
ListNode *cur = head;
while (cur) {
while (cur->next && cur->val == cur->next->val)
cur->next = cur->next->next;
cur = cur->next;
}
return head;
}
|
BM16 删除有序链表中重复的元素-II
删除有序链表中重复的元素-II_牛客题霸_牛客网 (nowcoder.com)
给出一个升序排序的链表,删除链表中的所有重复出现的元素,只保留原链表中只出现一次的元素。
例如:
给出的链表为1→2→3→3→4→4→51→2→3→3→4→4→5, 返回1→2→51→2→5.
给出的链表为1→1→1→2→31→1→1→2→3, 返回2→32→3.
示例1
输入:
{1,2,2}
返回值:
{1}
示例2
输入:
{}
返回值:
{}
题解:
想法都差不多,不过没做出来,学习学习
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
ListNode* deleteDuplicates(ListNode* head) {
// write code here
ListNode *pre = new ListNode(0);
pre->next = head;
ListNode *cur = pre;
while (cur->next && cur->next->next) {
if (cur->next->val == cur->next->next->val) {
int temp = cur->next->val;
while (cur->next && cur->next ->val == temp)
cur->next = cur->next->next;
}
else {
cur = cur->next;
}
}
return pre->next;
}
|
BM17 二分查找-1
二分查找-I_牛客题霸_牛客网 (nowcoder.com)
描述
请实现无重复数字的升序数组的二分查找
给定一个 元素升序的、无重复数字的整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标(下标从 0 开始),否则返回 -1
示例1
输入:
[-1,0,3,4,6,10,13,14],13
返回值:
6
说明:
13 出现在nums中并且下标为 6
示例2
输入:
[],3
返回值:
-1
说明:
nums为空,返回-1
示例3
输入:
[-1,0,3,4,6,10,13,14],2
返回值:
-1
说明:
2 不存在nums中因此返回 -1
备注:
数组元素长度在[0,10000]之间
数组每个元素都在 [-9999, 9999]之间。
题解:
如标题,二分查找,注意条件left <= right
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
int search(vector<int>& nums, int target) {
// write code here
if (nums.size() == 0)
return -1;
int left = 0, right = nums.size() - 1;
int mid = left + ((right - left) >> 1);
while (left <= right) {
if (nums[mid] > target)
right = mid - 1;
else if (nums[mid] < target)
left = mid + 1;
else
return mid;
mid = left + ((right - left) >> 1);
}
return -1;
}
|
BM19 寻找峰值
寻找峰值_牛客题霸_牛客网 (nowcoder.com)
描述
给定一个长度为n的数组nums,请你找到峰值并返回其索引。数组可能包含多个峰值,在这种情况下,返回任何一个所在位置即可。
1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于
2.假设 nums[-1] = nums[n] = −∞−∞
3.对于所有有效的 i 都有 nums[i] != nums[i + 1]
4.你可以使用O(logN)的时间复杂度实现此问题吗?
如输入[2,4,1,2,7,8,4]时,会形成两个山峰,一个是索引为1,峰值为4的山峰,另一个是索引为5,峰值为8的山峰,如下图所示:

示例1
输入:
[2,4,1,2,7,8,4]
返回值:
1
说明:
4和8都是峰值元素,返回4的索引1或者8的索引5都可以
示例2
输入:
[1,2,3,1]
返回值:
2
说明:
3 是峰值元素,返回其索引 2
题解:
二分法,一直往高处走,右边小的话,就更新right,左边小的话就更新left,直到相遇
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
int findPeakElement(vector<int>& nums) {
// write code here
if (nums.size() == 0)
return -1;
int left = 0, right = nums.size() - 1;
while (left < right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] > nums[mid + 1])
right = mid;
else
left = mid + 1;
}
return right;
}
|
BM20 数组中的逆序对
数组中的逆序对_牛客题霸_牛客网 (nowcoder.com)
描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P mod 1000000007
输入描述:
题目保证输入的数组中没有的相同的数字
示例1
输入:
[1,2,3,4,5,6,7,0]
返回值:
7
示例2
输入:
[1,2,3]
返回值:
0
题解:
归并排序,注意一下merge的逻辑,得多练练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
const int mod = 1000000007;
int InversePairs(vector<int>& nums) {
// write code here
if (nums.size() == 0)
return 0;
int ret = 0;
int l = 0, r = nums.size() - 1;
vector<int> help(nums.size(), 0);
mergeSort(nums, help, l, r, ret);
return ret;
}
void mergeSort(vector<int> &nums, vector<int> &help, int l, int r, int &ret) {
if (l >= r)
return;
int m = l + ((r - l) >> 1);
mergeSort(nums, help, l, m, ret);
mergeSort(nums, help, m + 1, r, ret);
merge(nums, help, l, m, r, ret);
}
void merge(vector<int> &nums, vector<int> &help, int l, int m, int r, int &ret) {
int i = l, j = m + 1, k = 0;
while (i <= m && j <= r) {
if (nums[i] > nums[j]) {
ret +=(m - i + 1);
help[k++] = nums[j++];
ret %= mod;
}
else
help[k++] = nums[i++];
}
while (i <= m)
help[k++] = nums[i++];
while (j <= r)
help[k++] = nums[j++];
for (k = 0, i = l; i <= r; ++i, ++k) {
nums[i] = help[k];
}
}
|
BM21 旋转数组的最小数字
旋转数组的最小数字_牛客题霸_牛客网 (nowcoder.com)
描述
有一个长度为 n 的非降序数组,比如[1,2,3,4,5],将它进行旋转,即把一个数组最开始的若干个元素搬到数组的末尾,变成一个旋转数组,比如变成了[3,4,5,1,2],或者[4,5,1,2,3]这样的。请问,给定这样一个旋转数组,求数组中的最小值。
示例1
输入:
[3,4,5,1,2]
返回值:
1
示例2
输入:
[3,100,200,3]
返回值:
3
题解:
二分查找,和右边作比较,大于则把左边拉过来,等于则把右边减一,小于则把右边拉过来,直到left和right相遇
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int minNumberInRotateArray(vector<int>& nums) {
// write code here
if (nums.size() == 0)
return -1;
int left = 0, right = nums.size() - 1;
while (left < right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] > nums[right])
left = mid + 1;
else if (nums[mid] == nums[right])
right--;
else
right = mid;
}
return nums[left];
}
|
BM22 比较版本号
比较版本号_牛客题霸_牛客网 (nowcoder.com)
描述
牛客项目发布项目版本时会有版本号,比如1.02.11,2.14.4等等
现在给你2个版本号version1和version2,请你比较他们的大小
版本号是由修订号组成,修订号与修订号之间由一个".“连接。1个修订号可能有多位数字组成,修订号可能包含前导0,且是合法的。例如,1.02.11,0.1,0.2都是合法的版本号
每个版本号至少包含1个修订号。
修订号从左到右编号,下标从0开始,最左边的修订号下标为0,下一个修订号下标为1,以此类推。
比较规则:
一. 比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较忽略任何前导零后的整数值。比如"0.1"和"0.01"的版本号是相等的
二. 如果版本号没有指定某个下标处的修订号,则该修订号视为0。例如,“1.1"的版本号小于"1.1.1”。因为"1.1"的版本号相当于"1.1.0”,第3位修订号的下标为0,小于1
三. version1 > version2 返回1,如果 version1 < version2 返回-1,不然返回0.
示例1
输入:
"1.1","2.1"
返回值:
-1
说明:
version1 中下标为 0 的修订号是 "1",version2 中下标为 0 的修订号是 "2" 。1 < 2,所以 version1 < version2,返回-1
示例2
输入:
"1.1","1.01"
返回值:
0
说明:
version2忽略前导0,为"1.1",和version相同,返回0
示例3
输入:
"1.1","1.1.1"
返回值:
-1
说明:
"1.1"的版本号小于"1.1.1"。因为"1.1"的版本号相当于"1.1.0",第3位修订号的下标为0,小于1,所以version1 < version2,返回-1
示例4
输入:
"2.0.1","2"
返回值:
1
说明:
version1的下标2>version2的下标2,返回1
示例5
输入:
"0.226","0.36"
返回值:
1
说明:
226>36,version1的下标2>version2的下标2,返回1
题解:
双指针,获取并转化成数字然后比较就可以了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
int compare(string version1, string version2) {
// write code here
int n1 = version1.size(), n2 = version2.size();
int i = 0, j = 0;
while (i < n1 || j < n2) {
int num1 = 0, num2 = 0;
while (i < n1 && version1[i] != '.') {
num1 = num1 *10 + (version1[i] - '0');
i++;
}
i++;
while (j < n2 && version2[j] != '.' ) {
num2 = num2 *10 + (version2[j] - '0');
j++;
}
j++;
if (num1 > num2)
return 1;
else if (num1 < num2)
return -1;
}
return 0;
}
|
BM23 二叉树的前序遍历
二叉树的前序遍历_牛客题霸_牛客网 (nowcoder.com)
描述
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
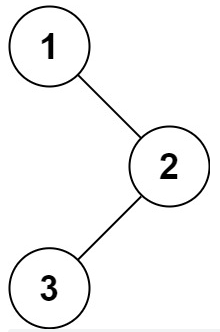
示例1
输入:
{1,#,2,3}
返回值:
[1,2,3]
题解:
递归调用,没什么好说的,注意一下递归退出条件。
1
2
3
4
5
6
7
8
9
10
|
vector<int> ans;
vector<int> preorderTraversal(TreeNode* root) {
// write code here
if (root == nullptr)
return vector<int> ();
ans.push_back(root->val);
preorderTraversal(root->left);
preorderTraversal(root->right);
return ans;
}
|
BM24 二叉树的中序遍历
二叉树的中序遍历_牛客题霸_牛客网 (nowcoder.com)
描述都不放了,直接题解:
1
2
3
4
5
6
7
8
9
10
|
vector<int> ans;
vector<int> inorderTraversal(TreeNode* root) {
// write code here
if (root == nullptr)
return ans;
inorderTraversal(root->left);
ans.push_back(root->val);
inorderTraversal(root->right);
return ans;
}
|
BM25 二叉树的后序遍历
没啥好说的,水题,不过可以练练非递归遍历,这里先写个递归
1
2
3
4
5
6
7
8
9
10
|
vector<int> ans;
vector<int> postorderTraversal(TreeNode* root) {
// write code here
if (root == nullptr)
return ans;
postorderTraversal(root->left);
postorderTraversal(root->right);
ans.push_back(root->val);
return ans;
}
|
BM28 二叉树的最大深度
描述
求给定二叉树的最大深度,
深度是指树的根节点到任一叶子节点路径上节点的数量。
最大深度是所有叶子节点的深度的最大值。
(注:叶子节点是指没有子节点的节点。)
示例1
输入:
{1,2}
返回值:
2
示例2
输入:
{1,2,3,4,#,#,5}
返回值:
3
题解:
有点尴尬了,飘了点,不过依然是递归的问题,可以练练非递归思路,打开思维
1
2
3
4
5
6
|
int maxDepth(TreeNode* root) {
// write code here
if (root == nullptr)
return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
|
BM30 二叉搜索树与双向链表
二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)
描述
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示

注意:
1.要求不能创建任何新的结点,只能调整树中结点指针的指向。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode,有左右指针,其实可以看成一个双向链表的数据结构
4.你不用输出双向链表,程序会根据你的返回值自动打印输出
输入描述:
二叉树的根节点
返回值描述:
双向链表的其中一个头节点。
示例1
输入:
{10,6,14,4,8,12,16}
返回值:
From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;
说明:
输入题面图中二叉树,输出的时候将双向链表的头节点返回即可。
示例2
输入:
{5,4,#,3,#,2,#,1}
返回值:
From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;
说明:
5
/
4
/
3
/
2
/
1
树的形状如上图
题解:
其实就是二叉树的中序变量,变体而已,思路是对的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
TreeNode *pre = nullptr;
TreeNode *head = nullptr;
TreeNode* Convert(TreeNode* pRootOfTree) {
if (pRootOfTree == nullptr)
return nullptr;
Convert(pRootOfTree->left);
if (pre == nullptr) {
pre = pRootOfTree;
head = pRootOfTree;
}
else {
pre->right =pRootOfTree;
pRootOfTree->left = pre;
pre = pRootOfTree;
}
Convert(pRootOfTree->right);
return head;
}
|
BM32 合并二叉树
合并二叉树_牛客题霸_牛客网 (nowcoder.com)
描述
已知两颗二叉树,将它们合并成一颗二叉树。合并规则是:都存在的结点,就将结点值加起来,否则空的位置就由另一个树的结点来代替。例如:
两颗二叉树是:
Tree 1
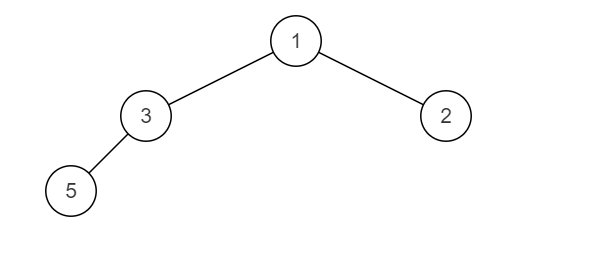
Tree 2
 合并后的树为
合并后的树为
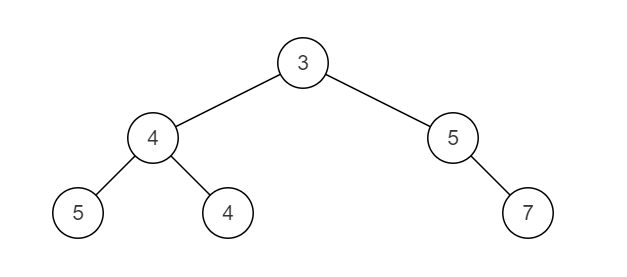
示例1
输入:
{1,3,2,5},{2,1,3,#,4,#,7}
返回值:
{3,4,5,5,4,#,7}
说明:
如题面图
示例2
输入:
{1},{}
返回值:
{1}
题解:
还是二叉树的递归,没啥好说的
1
2
3
4
5
6
7
8
9
10
|
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
// write code here
if (t1 == nullptr || t2 == nullptr)
return t1 ? t1 : t2;
if (t1 != nullptr && t2 != nullptr)
t1->val += t2 ->val;
t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);
return t1;
}
|
BM33 二叉树的镜像
二叉树的镜像_牛客题霸_牛客网 (nowcoder.com)
描述
操作给定的二叉树,将其变换为源二叉树的镜像。
比如:
源二叉树

镜像二叉树

示例1
输入:
{8,6,10,5,7,9,11}
返回值:
{8,10,6,11,9,7,5}
说明:
如题面所示
示例2
输入:
{}
返回值:
{}
题解:
照样是二叉树递归交换一下左右就OK
1
2
3
4
5
6
7
8
9
10
|
TreeNode* Mirror(TreeNode* pRoot) {
// write code here
if (pRoot == nullptr)
return nullptr;
TreeNode *leftNode = Mirror(pRoot->right);
TreeNode *rightNode = Mirror(pRoot->left);
pRoot->left = leftNode;
pRoot->right = rightNode;
return pRoot;
}
|
BM34 判断是不是二叉搜索树
判断是不是二叉搜索树_牛客题霸_牛客网 (nowcoder.com)
描述
给定一个二叉树根节点,请你判断这棵树是不是二叉搜索树。
二叉搜索树满足每个节点的左子树上的所有节点均小于当前节点且右子树上的所有节点均大于当前节点。
例:
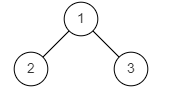
图1
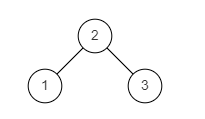
图2
示例1
输入:
{1,2,3}
返回值:
false
说明:
如题面图1
示例2
输入:
{2,1,3}
返回值:
true
说明:
如题面图2
题解:
其实依然是二叉树的递归,不过可能更绕了,得注意一下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
long pre = LONG_MIN;
bool isValidBST(TreeNode* root) {
// write code here
if (root == nullptr)
return true;
if (!isValidBST(root->left))
return false;
if (root->val <= pre)
return false;
pre = root->val;
if (!isValidBST(root->right))
return false;
return true;
}
|
BM35 判断是不是完全二叉树
判断是不是完全二叉树_牛客题霸_牛客网 (nowcoder.com)
描述
给定一个二叉树,确定他是否是一个完全二叉树。
完全二叉树的定义:若二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大个数,第 h 层所有的叶子结点都连续集中在最左边,这就是完全二叉树。(第 h 层可能包含 [1~2h] 个节点)
样例图1:
样例图2:
样例图3:
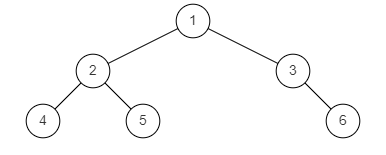
示例1
输入:
{1,2,3,4,5,6}
返回值:
true
示例2
输入:
{1,2,3,4,5,6,7}
返回值:
true
示例3
输入:
{1,2,3,4,5,#,6}
返回值:
false
题解:
第一版,其实这道题有更优解不过忘了咋做,反正大概是保存层级,这里用了队列,下次优化优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
bool isCompleteTree(TreeNode* root) {
// write code here
if (root == nullptr)
return true;
queue<TreeNode*> que;
que.push(root);
bool flag = false;
while ( !que.empty()) {
int sz = que.size();
for (int i = 0; i < sz; i++) {
TreeNode *cur = que.front();
que.pop();
if (cur == nullptr)
flag = true;
else {
if (flag) return false;
que.push(cur->left);
que.push(cur->right);
}
}
}
return true;
}
|
BM36 判断是不是平衡二叉树
判断是不是平衡二叉树_牛客题霸_牛客网 (nowcoder.com)
描述
输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。
在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树
平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
样例解释:
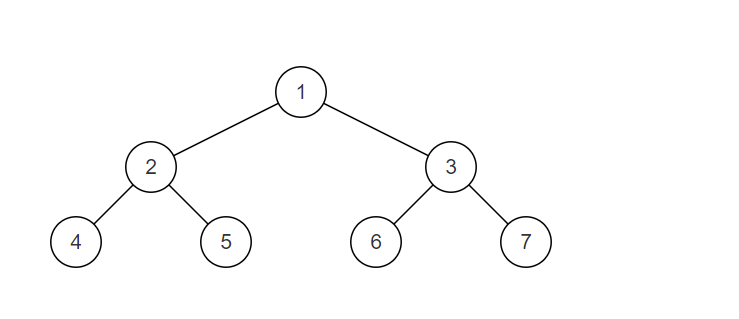
样例二叉树如图,为一颗平衡二叉树
注:我们约定空树是平衡二叉树。
输入描述:
输入一棵二叉树的根节点
返回值描述:
输出一个布尔类型的值
示例1
输入:
{1,2,3,4,5,6,7}
返回值:
true
示例2
输入:
{}
返回值:
true
题解:
经典的树形DP,可以用套路解决,即向左右子树要信息,也可以看看官方题解,拓展拓展思路
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class ReturnType {
public:
ReturnType(bool isb, int he){
isB = isb;
height = he;
}
bool isB;
int height;
};
ReturnType * process(TreeNode *root) {
if (root == nullptr)
return new ReturnType(true, 0);
ReturnType *leftdata = process(root->left);
ReturnType *rightdata = process(root->right);
int height = max(leftdata->height, rightdata->height) + 1;
bool isBalanced = leftdata->isB && rightdata->isB &&
abs(leftdata->height - rightdata->height) <= 1;
delete leftdata;
delete rightdata;
return new ReturnType(isBalanced, height);
}
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pRoot TreeNode类
* @return bool布尔型
*/
bool IsBalanced_Solution(TreeNode* pRoot) {
// write code here
return process(pRoot)->isB;
}
|
BM37 二叉搜索树的最近公共祖先
二叉搜索树的最近公共祖先_牛客题霸_牛客网 (nowcoder.com)
描述
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
1.对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q,最近公共祖先LCA(T,p,q)表示一个节点x,满足x是p和q的祖先且x的深度尽可能大。在这里,一个节点也可以是它自己的祖先.
2.二叉搜索树是若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值
3.所有节点的值都是唯一的。
4.p、q 为不同节点且均存在于给定的二叉搜索树中。
数据范围:
3<=节点总数<=10000
0<=节点值<=10000
如果给定以下搜索二叉树: {7,1,12,0,4,11,14,#,#,3,5},如下图:

示例1
输入:
{7,1,12,0,4,11,14,#,#,3,5},1,12
返回值:
7
说明:
节点1 和 节点12的最近公共祖先是7
示例2
输入:
{7,1,12,0,4,11,14,#,#,3,5},12,11
返回值:
12
说明:
因为一个节点也可以是它自己的祖先.所以输出12
题解:
依旧是二叉树的DP问题,只需要看看节点是否在自己两侧,是的话就是了,不是的话看看在哪一侧,然后递归求解
1
2
3
4
5
6
7
8
9
10
11
12
|
int lowestCommonAncestor(TreeNode* root, int p, int q) {
// write code here
if (root == nullptr)
return -1;
if (p >= root->val && q <= root->val || p <= root->val && q >= root->val)
return root->val;
else if (p <= root->val && q <= root->val)
return lowestCommonAncestor(root->left, p, q);
else
return lowestCommonAncestor(root->right, p, q);
return -1;
}
|
BM38 在二叉树中找到两个节点的最近公共祖先
在二叉树中找到两个节点的最近公共祖先_牛客题霸_牛客网 (nowcoder.com)
描述
给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2,请找到 o1 和 o2 的最近公共祖先节点。
注:本题保证二叉树中每个节点的val值均不相同。
如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时,二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示:

所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3,所以对应的输出为3。
节点本身可以视为自己的祖先
示例1
输入:
{3,5,1,6,2,0,8,#,#,7,4},5,1
返回值:
3
示例2
输入:
{3,5,1,6,2,0,8,#,#,7,4},2,7
返回值:
2
题解:
更是经典的树形DP。如果当前节点就是其中之一,则返回当前节点,如果当前节点左右两侧是目标,说明当前节点是公共祖先,则返回当前节点,其余情况看看代码就懂了
1
2
3
4
5
6
7
8
9
10
11
12
13
|
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
// write code here
if (root == nullptr)
return 0;
if (root->val == o1 || root->val == o2)
return root->val;
int leftdata = lowestCommonAncestor(root->left, o1, o2);
int rightdata = lowestCommonAncestor(root->right, o1, o2);
if (leftdata && rightdata)
return root->val;
else
return leftdata ? leftdata : rightdata;
}
|
BM39 序列化二叉树
描述
请实现两个函数,分别用来序列化和反序列化二叉树,不对序列化之后的字符串进行约束,但要求能够根据序列化之后的字符串重新构造出一棵与原二叉树相同的树。
二叉树的序列化(Serialize)是指:把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串,从而使得内存中建立起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序的二叉树等遍历方式来进行修改,序列化的结果是一个字符串,序列化时通过 某种符号表示空节点(#)
二叉树的反序列化(Deserialize)是指:根据某种遍历顺序得到的序列化字符串结果str,重构二叉树。
例如,可以根据层序遍历的方案序列化,如下图:

层序序列化(即用函数Serialize转化)如上的二叉树转为"{1,2,3,#,#,6,7}",再能够调用反序列化(Deserialize)将"{1,2,3,#,#,6,7}“构造成如上的二叉树。
当然你也可以根据满二叉树结点位置的标号规律来序列化,还可以根据先序遍历和中序遍历的结果来序列化。不对序列化之后的字符串进行约束,所以欢迎各种奇思妙想。
示例1
输入:
{1,2,3,#,#,6,7}
返回值:
{1,2,3,#,#,6,7}
说明:
如题面图
示例2
输入:
{8,6,10,5,7,9,11}
返回值:
{8,6,10,5,7,9,11}
题解:
序列化:其实就是二叉树的前序遍历,并且用,做分隔符,先将当前节点的$val$用to_string()方法转换成string然后追加到string后,进行先序遍历。
反序列化:相当于二叉树的重建,判断当前的str的值是不是#,是的话直接返回空节点,将string的值转化成int类型的$val$然后new一个节点当做当前的根节点,前序遍历构建根节点的左右子节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
void SeralizeFunc(TreeNode *root, string &str) {
if (root == nullptr) {
str += '#';
return;
}
string temp = to_string(root->val);
str += temp + ',';
SeralizeFunc(root->left, str);
SeralizeFunc(root->right, str);
}
char* Serialize(TreeNode *root) {
if (root == nullptr) return "#";
string res;
SeralizeFunc(root, res);
char *charRes = new char[res.length() + 1];
strcpy(charRes, res.c_str());
charRes[res.length()] = '\0';
return charRes;
}
TreeNode *DeserializeFunc(char **str) {
if (**str == '#') {
(*str)++;
return nullptr;
}
int val = 0;
while (**str != ',' && **str != '\0') {
val = val *10 + ((**str) - '0');
(*str)++;
}
TreeNode *root = new TreeNode(val);
if (**str == '\0') return root;
else (*str)++;
root->left = DeserializeFunc(str);
root->right = DeserializeFunc(str);
return root;
}
TreeNode* Deserialize(char *str) {
if (str == "#") return nullptr;
TreeNode *res = DeserializeFunc(&str);
return res;
}
|
BM40 重建二叉树
重建二叉树_牛客题霸_牛客网 (nowcoder.com)
描述
给定节点数为 n 的二叉树的前序遍历和中序遍历结果,请重建出该二叉树并返回它的头结点。
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建出如下图所示。

提示:
1.vin.length == pre.length
2.pre 和 vin 均无重复元素
3.vin出现的元素均出现在 pre里
4.只需要返回根结点,系统会自动输出整颗树做答案对比
示例1
输入:
[1,2,4,7,3,5,6,8],[4,7,2,1,5,3,8,6]
返回值:
{1,2,3,4,#,5,6,#,7,#,#,8}
说明:
返回根节点,系统会输出整颗二叉树对比结果,重建结果如题面图示
示例2
输入:
[1],[1]
返回值:
{1}
示例3
输入:
[1,2,3,4,5,6,7],[3,2,4,1,6,5,7]
返回值:
{1,2,5,3,4,6,7}
题解:
麻了,重点就是leftsize(左子树节点个数)我想直接用index但是显然不行,好好看看
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
TreeNode *buildTree(vector<int> &preOrder, int l1, int r1, vector<int> &vinOrder, int l2, int r2) {
if (l1 > r1 || l2 > r2)
return nullptr;
TreeNode *root = new TreeNode(preOrder[l1]);
int index = l2;
while (index <= r2) {
if (preOrder[l1] == vinOrder[index])
break;
index++;
}
int leftsize = index - l2; //重点
root->left = buildTree(preOrder, l1 + 1, l1 + leftsize , vinOrder, l2, index - 1);
root->right = buildTree(preOrder, l1 + leftsize + 1, r1, vinOrder, index + 1, r2);
return root;
}
TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {
// write code here
if (preOrder.empty() || vinOrder.empty())
return nullptr;
TreeNode *root = buildTree(preOrder, 0, preOrder.size() - 1, vinOrder, 0, vinOrder.size() - 1);
return root;
}
|
BM41 输出二叉树的右视图
输出二叉树的右视图_牛客题霸_牛客网 (nowcoder.com)
描述
请根据二叉树的前序遍历,中序遍历恢复二叉树,并打印出二叉树的右视图
如输入[1,2,4,5,3],[4,2,5,1,3]时,通过前序遍历的结果[1,2,4,5,3]和中序遍历的结果[4,2,5,1,3]可重建出以下二叉树:

所以对应的输出为[1,3,5]。
示例1
输入:
[1,2,4,5,3],[4,2,5,1,3]
返回值:
[1,3,5]
备注:
二叉树每个节点的值在区间[1,10000]内,且保证每个节点的值互不相同。
题解:
先建树,然后用队列层序遍历,每次保存最后一个节点的值(用size来实现)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
unordered_map<int, int> mp;
TreeNode *buildTree(vector<int> &preOrder, int l1, int r1, vector<int> &inOrder, int l2, int r2) {
if (l1 > r1 || l2 > r2)
return nullptr;
int preOrder_root = l1;
int inOrder_root = mp[preOrder[preOrder_root]];
TreeNode *root = new TreeNode(preOrder[preOrder_root]);
int leftsize = inOrder_root - l2;
root->left = buildTree(preOrder, l1 + 1, l1 + leftsize, inOrder, l2, inOrder_root - 1);
root->right = buildTree(preOrder, l1 + leftsize + 1, r1, inOrder, inOrder_root + 1, r2);
return root;
}
vector<int> rightView(TreeNode *root) {
vector<int> res;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()) {
int size = q.size();
while (size--) {
TreeNode *temp = q.front();
q.pop();
if (temp->left)
q.push(temp->left);
if (temp->right)
q.push(temp->right);
if (size == 0)
res.push_back(temp->val);
}
}
return res;
}
vector<int> solve(vector<int>& preOrder, vector<int>& inOrder) {
// write code here
if (preOrder.size() == 0 || inOrder.size() == 0)
return {};
for (int i = 0; i < preOrder.size(); i++)
mp[inOrder[i]] = i; //折腾我很久的问题,之前写的mp[preOrder[i]] = i;显然不对啊,存的是中序的索引
TreeNode *root = buildTree(preOrder, 0, preOrder.size() - 1, inOrder, 0, inOrder.size() - 1);
return rightView(root);
}
|
BM42 用两个栈实现队列
用两个栈实现队列_牛客题霸_牛客网 (nowcoder.com)
描述
用两个栈来实现一个队列,使用n个元素来完成 n 次在队列尾部插入整数(push)和n次在队列头部删除整数(pop)的功能。 队列中的元素为int类型。保证操作合法,即保证pop操作时队列内已有元素。
示例1
输入:
["PSH1","PSH2","POP","POP"]
返回值:
1,2
说明:
"PSH1":代表将1插入队列尾部
"PSH2":代表将2插入队列尾部
"POP“:代表删除一个元素,先进先出=>返回1
"POP“:代表删除一个元素,先进先出=>返回2
示例2
输入:
["PSH2","POP","PSH1","POP"]
返回值:
2,1
题解:
很简单的逻辑
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution
{
public:
void push(int node) {
stack1.push(node);
}
int pop() {
if (stack2.empty()) {
while (!stack1.empty()) {
stack2.push(stack1.top());
stack1.pop();
}
}
int res = stack2.top();
stack2.pop();
return res;
}
private:
stack<int> stack1;
stack<int> stack2;
};
|
BM43 包含min函数的栈
包含min函数的栈_牛客题霸_牛客网 (nowcoder.com)
描述就不粘贴了
题解:主要就是用一个辅助栈空间保存最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
stack<int> mindata, data;
void push(int value) {
if (mindata.empty() || value <= mindata.top())
mindata.push(value);
data.push(value);
}
void pop() {
if (mindata.top() == data.top())
mindata.pop();
data.pop();
}
int top() {
return data.top();
}
int min() {
return mindata.top();
}
};
|
BM44 有效括号序列
有效括号序列_牛客题霸_牛客网 (nowcoder.com)
描述
给出一个仅包含字符’(’,’)’,’{’,’}’,’[‘和’]’,的字符串,判断给出的字符串是否是合法的括号序列
括号必须以正确的顺序关闭,”()“和”()[]{}“都是合法的括号序列,但”(]“和”([)]“不合法。
示例1
输入:
"["
返回值:
false
示例2
输入:
"[]"
返回值:
true
题解:
用栈来保存状态,(其实在计算机内部也是用栈来保存各种状态)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
bool isValid(string s) {
// write code here
if (s.size() < 2)
return false;
stack<char> help;
for (char c : s) {
if (c == '(') help.push(')');
else if (c == '[') help.push(']');
else if (c == '{') help.push('}');
else if (help.empty()) return false; //这里注意了,如果不加的话下一行可能越界
else if (c == help.top())
help.pop();
}
return help.empty();
}
|
BM45 滑动窗口的最大值
滑动窗口的最大值_牛客题霸_牛客网 (nowcoder.com)
描述
给定一个长度为 n 的数组 num 和滑动窗口的大小 size ,找出所有滑动窗口里数值的最大值。
例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
窗口大于数组长度或窗口长度为0的时候,返回空。
示例1
输入:
[2,3,4,2,6,2,5,1],3
返回值:
[4,4,6,6,6,5]
示例2
输入:
[9,10,9,-7,-3,8,2,-6],5
返回值:
[10,10,9,8]
示例3
输入:
[1,2,3,4],5
返回值:
[]
题解:
有很多细节
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
void findMax(vector<int> &num, int left, int right,int &maxNum, int &maxIndex) {
maxNum = INT_MIN; //不能少,因为要更新最大值,如果不这样可能一直都是一个值不会被覆盖
while (left <= right) {
if (num[left] > maxNum) {
maxNum = num[left];
maxIndex = left;
}
left++;
}
}
vector<int> maxInWindows(vector<int>& num, int size) {
// write code here
int len = num.size();
vector<int> ans;
if (len == 0 || size == 0 || len < size)
return ans;
int left = 0, right = size - 1;
int maxNum = INT_MIN;
int maxIndex = 0;
findMax(num, left, right,maxNum, maxIndex);
while (right < len) {
if (maxIndex < left)
findMax(num, left, right, maxNum, maxIndex);
if (num[right] > maxNum) {
maxIndex = right;
maxNum = num[maxIndex];
}
ans.push_back(maxNum);
right++;
left++;
}
return ans;
}
|
BM47 寻找第K大
寻找第K大_牛客题霸_牛客网 (nowcoder.com)
描述
有一个整数数组,请你根据快速排序的思路,找出数组中第 k 大的数。
给定一个整数数组 a ,同时给定它的大小n和要找的 k ,请返回第 k 大的数(包括重复的元素,不用去重),保证答案存在。
示例1
输入:
[1,3,5,2,2],5,3
返回值:
2
复制
示例2
输入:
[10,10,9,9,8,7,5,6,4,3,4,2],12,3
返回值:
9
说明:
去重后的第3大是8,但本题要求包含重复的元素,不用去重,所以输出9
题解:
快排改进(不用一定排序完,只要找到下标为n-k那个正确的元素就可以了)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
int quickSelect(vector<int> &nums, int l, int r, int k) {
if (l == r)
return nums[k];
int partition = nums[l], less = l - 1, more = r + 1;
while (less < more) {
do less++; while (nums[less] < partition);
do more--; while (nums[more] > partition);
if (less < more)
swap(nums[less], nums[more]);
}
if (k <= more)
return quickSelect(nums, l, more, k);
else
return quickSelect(nums, more + 1, r, k);
}
int findKth(vector<int>& a, int n, int K) {
// write code here
return quickSelect(a,0, n - 1, n-K);
}
|
BM48 数据流的中位数
数据流中的中位数_牛客题霸_牛客网 (nowcoder.com)
描述
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流,使用GetMedian()方法获取当前读取数据的中位数。
示例1
输入:
[5,2,3,4,1,6,7,0,8]
返回值:
"5.00 3.50 3.00 3.50 3.00 3.50 4.00 3.50 4.00 "
说明:
数据流里面不断吐出的是5,2,3...,则得到的平均数分别为5,(5+2)/2,3...
示例2
输入:
[1,1,1]
返回值:
"1.00 1.00 1.00 "
题解:
之前用的排序,非常的操蛋,现在改成大根堆小根堆来做
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
priority_queue<int> min_q;
priority_queue<int, vector<int>, greater<int>> max_q;
void Insert(int num) {
min_q.push(num);
max_q.push(min_q.top());
min_q.pop();
if (min_q.size() < max_q.size()) {
min_q.push(max_q.top());
max_q.pop();
}
}
double GetMedian() {
return min_q.size() > max_q.size() ? static_cast<double>(min_q.top()) : static_cast<double>(min_q.top() + max_q.top()) / 2;
}
|
BM49 表达式求值
表达式求值_牛客题霸_牛客网 (nowcoder.com)
描述
请写一个整数计算器,支持加减乘三种运算和括号。
示例1
输入:
"1+2"
返回值:
3
示例2
输入:
"(2*(3-4))*5"
返回值:
-10
示例3
输入:
"3+2*3*4-1"
返回值:
26
题解:
有点复杂了啊,主要是用好栈,处理好优先级和各种逻辑
这里有个优秀题解可以看看:【宫水三叶の真题精选】使用「双栈」解决「究极表达式计算」问题(含拓展)_牛客博客 (nowcoder.net)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
vector<int> process(string s, int index) {
stack<int> st;
int num = 0;
char op = '+';
int i;
for (i = index; i < s.size(); ++i) {
if (isdigit(s[i])) {
num = num * 10 + s[i] - '0';
if (i != s.size() - 1)
continue;
}
if (s[i] == '(') {
vector<int> res = process(s, i + 1);
num = res[0];
i = res[1];
if (i != s.size() - 1)
continue;
}
switch(op) {
case '+':
st.push(num);
break;
case '-':
st.push(-num);
break;
case '*':
int temp = st.top();
st.pop();
st.push(temp * num);
break;
}
num = 0;
if (s[i] == ')')
break;
else
op = s[i];
}
int sum = 0;
while (!st.empty()) {
sum += st.top();
st.pop();
}
return vector<int> {sum, i};
}
int solve(string s) {
// write code here
return process(s, 0)[0];
}
|
BM51 数组中出现次数超过一半的数字
数组中出现次数超过一半的数字_牛客题霸_牛客网 (nowcoder.com)
描述
给一个长度为 n 的数组,数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
例如输入一个长度为9的数组[1,2,3,2,2,2,5,4,2]。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。
输入描述:
保证数组输入非空,且保证有解
示例1
输入:
[1,2,3,2,2,2,5,4,2]
返回值:
2
示例2
输入:
[3,3,3,3,2,2,2]
返回值:
3
示例3
输入:
[1]
返回值:
1
题解:
如果直接用哈希表,那就没什么好说的了,用一个map即可搞定,不过空间复杂度O(n),解题简单最优解难啊。
这里的解法挺优雅,候选排除法,相当于对题目性质(超过数组长度的一半)的利用了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
int MoreThanHalfNum_Solution(vector<int>& numbers) {
// write code here
int cnt = 0;
int cond = -1;
for (int i = 0; i < numbers.size(); ++i) {
if (cnt == 0) {
cond = numbers[i];
++cnt;
}
else {
if (numbers[i] == cond) ++cnt;
else --cnt;
}
}
cnt = 0;
for (const int i : numbers) {
if (i == cond)
++cnt;
}
if (cnt > numbers.size() / 2) return cond;
return 0;
}
|
BM52 数组中只出现一次的两个数字
数组中只出现一次的两个数字_牛客题霸_牛客网 (nowcoder.com)
描述
一个整型数组里除了两个数字只出现一次,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。
提示:输出时按非降序排列。
示例1
输入:
[1,4,1,6]
返回值:
[4,6]
说明:
返回的结果中较小的数排在前面
示例2
输入:
[1,2,3,3,2,9]
返回值:
[1,9]
题解:
这道题也是很巧妙的一道题了,位运算,当然用哈希表一样可以解决(O(n))。用位运算只需要O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
vector<int> findDigit(vector<int> &nums) {
int num1 = 0;
for (const int a : nums)
num1 ^= a;
int rightOne = num1 & (~num1 + 1);
int num2 = 0;
for (const int b : nums) {
if (b & rightOne)
num2 ^= b;
}
num1 ^= num2;
return {min(num1, num2), max(num1, num2)};
}
vector<int> FindNumsAppearOnce(vector<int>& nums) {
// write code here
return findDigit(nums);
}
|
BM53 缺失的第一个正整数
缺失的第一个正整数_牛客题霸_牛客网 (nowcoder.com)
题解:
已经是第二次碰到这个题了,大概思路知道了,不过发现了一个小细节
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
int minNumberDisappeared(vector<int>& nums) {
// write code here
int n = nums.size();
for (int &i : nums) {
if (i <= 0)
i = n + 1;
}
for (int i = 0; i < n; i++) {
int num = abs(nums[i]); //一定要有这一步,因为nums[i]可能被标记为负
if (num <= n) {
nums[num - 1] = - abs(nums[num - 1]);
}
}
for (int i = 0; i < n ; i++) {
if (nums[i] > 0)
return i+1;
}
return n + 1;
}
|
BM55 没有重复项数字的全排列
没有重复项数字的全排列_牛客题霸_牛客网 (nowcoder.com)
描述
给出一组数字,返回该组数字的所有排列
例如:
[1,2,3]的所有排列如下
[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1].
(以数字在数组中的位置靠前为优先级,按字典序排列输出。)
示例1
输入:
[1,2,3]
返回值:
[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例2
输入:
[1]
返回值:
[[1]]
题解:
利用递归可以解决
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
vector<vector<int> > permute(vector<int>& num) {
// write code here
sort(num.begin(), num.end());
vector<vector<int>> res;
recursion(res, num, 0);
return res;
}
void recursion(vector<vector<int>> &res, vector<int> &num, int index) {
if (index == num.size())
res.push_back(num);
else {
for (int i = index; i < num.size(); ++i) {
swap(num[i], num[index]);
recursion(res, num, index + 1); //递归后续的
swap(num[i], num[index]);
}
}
}
|
BM56 有重复项数字的全排列
有重复项数字的全排列_牛客题霸_牛客网 (nowcoder.com)
描述
给出一组可能包含重复项的数字,返回该组数字的所有排列。结果以字典序升序排列。
示例1
输入:
[1,1,2]
返回值:
[[1,1,2],[1,2,1],[2,1,1]]
示例2
输入:
[0,1]
返回值:
[[0,1],[1,0]]
题解:
其实和上面的无重复项数字的全排列差不多,就是多了个判断是否用过而已
::回溯真的是我的硬伤啊,得狠狠刷起来
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
vector<vector<int> > permuteUnique(vector<int>& num) {
// write code here
sort(num.begin(), num.end());
vector<int> used(num.size(), 0);
vector<vector<int>> ans;
vector<int> temp;
backtrack(ans, num, temp, used);
return ans;
}
void backtrack(vector<vector<int>> &ans, vector<int> &num, vector<int> &temp, vector<int> used) {
if (temp.size() == num.size()) {
ans.push_back(temp);
return;
}
for (int i = 0; i < num.size(); ++i) {
if (used[i])
continue;
if (i > 0 && num[ i - 1] == num[i] && used[i - 1]) {
used[i] = 1;
continue;
}
used[i] = 1;
temp.push_back(num[i]);
backtrack(ans, num, temp, used);
used[i] = 0;
temp.pop_back();
}
}
|
BM57 岛屿数量
岛屿数量_牛客题霸_牛客网 (nowcoder.com)
描述
给一个01矩阵,1代表是陆地,0代表海洋, 如果两个1相邻,那么这两个1属于同一个岛。我们只考虑上下左右为相邻。
岛屿: 相邻陆地可以组成一个岛屿(相邻:上下左右) 判断岛屿个数。
例如:
输入
[
[1,1,0,0,0],
[0,1,0,1,1],
[0,0,0,1,1],
[0,0,0,0,0],
[0,0,1,1,1]
]
对应的输出为3
(注:存储的01数据其实是字符'0’,‘1’)
示例1
输入:
[[1,1,0,0,0],[0,1,0,1,1],[0,0,0,1,1],[0,0,0,0,0],[0,0,1,1,1]]
返回值:
3
示例2
输入:
[[0]]
返回值:
0
示例3
输入:
[[1,1],[1,1]]
返回值:
1
备注:
01矩阵范围<=200*200
题解:
图的dfs套路,其实是第二次做了,更熟悉了一点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
int solve(vector<vector<char> >& grid) {
// write code here
if (grid.size() == 0)
return 0;
int m = grid.size();
int n = grid[0].size();
int cnt = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == '1') {
++cnt;
dfs(grid, i, j);
}
}
}
return cnt;
}
void dfs(vector<vector<char>> &grid, int i, int j) {
if (i < 0 || j < 0 || i >= grid.size() || j >= grid[0].size())
return;
if (grid[i][j] == '1') {
grid[i][j] = '2';
dfs(grid, i + 1, j);
dfs(grid, i - 1, j);
dfs(grid, i, j - 1);
dfs(grid, i, j + 1);
}
}
|
BM58 字符串的排列
字符串的排列_牛客题霸_牛客网 (nowcoder.com)
描述
输入一个长度为 n 字符串,打印出该字符串中字符的所有排列,你可以以任意顺序返回这个字符串数组。
例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。

输入描述:
输入一个字符串,长度不超过10,字符只包括大小写字母。
示例1
输入:
"ab"
返回值:
["ab","ba"]
说明:
返回["ba","ab"]也是正确的
示例2
输入:
"aab"
返回值:
["aab","aba","baa"]
示例3
输入:
"abc"
返回值:
["abc","acb","bac","bca","cab","cba"]
复制
示例4
输入:
""
返回值:
[""]
题解:
和今天做的一个有重复数字的全排列很像,都是回溯法,得好好看看(感觉好多都是套路)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
vector<string> Permutation(string str) {
// write code here
vector<string> ans;
if (str.size() == 0)
return ans;
sort(str.begin(), str.end());
vector<int> used(str.size(), 0);
string temp;
backtrack(str, ans, used, temp);
return ans;
}
void backtrack(string &str, vector<string> &ans, vector<int> &used, string &temp) {
if (temp.size() == str.size()) {
ans.push_back(temp);
return;
}
for (int i = 0; i < str.size(); ++i) {
if (used[i])
continue;
if (i > 0 && str[i - 1] == str[i] && used[i - 1]) {
continue;
}
used[i] = 1;
temp.push_back(str[i]);
backtrack(str, ans, used, temp);
used[i] = 0;
temp.pop_back();
}
}
|


















 合并后的树为
合并后的树为














