平时刷
414 第三大的数
第三大的数
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。
示例 1:
输入:[3, 2, 1]
输出:1
解释:第三大的数是 1 。
示例 2:
输入:[1, 2]
输出:2
解释:第三大的数不存在, 所以返回最大的数 2 。
示例 3:
输入:[2, 2, 3, 1]
输出:1
解释:注意,要求返回第三大的数,是指在所有不同数字中排第三大的数。
此例中存在两个值为 2 的数,它们都排第二。在所有不同数字中排第三大的数为 1 。
题解:
可以创建三个变量,用来储存第一、第二、第三大的数,遍历一次数组O(n)即可实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
int thirdMax(vector<int>& nums) {
long long first = LONG_MIN, second = LONG_MIN, third = LONG_MIN;
for (auto &a : nums){ //遍历数组
if(a > first){ //最大的数
third = second;
second = first;
first = a;
}
else if(a < first && a > second){ //第二大的数
third = second;
second = a;
}
if(a > third && a < second){ //第三大的数
third = a;
}
}
if(third == LONG_MIN)
return first;
else
return third;
}
};
|
581最短无序连续子数组
581. 最短无序连续子数组 - 力扣(LeetCode)
给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组,并输出它的长度。
示例 1:
输入:nums = [2,6,4,8,10,9,15]
输出:5
解释:你只需要对 [6, 4, 8, 10, 9] 进行升序排序,那么整个表都会变为升序排序。
示例 2:
输入:nums = [1,2,3,4]
输出:0
示例 3:
输入:nums = [1]
输出:0
题解:
首先创建两个变量left和right分别来表示符合题意子数组的左右边界,两个变量max和min来表示遍历数组得到的最大值和最小值,设max初始值为nums[0],min初始值为nums[len-1]。
从nums[i] (i = 1)开始遍历数组,如果nums[i] > max说明nums[0~i]是升序,将max的值更新成nums[i],如果nums[i] < max,说明nums[0~(i-1)]是升序,可以不管前面那部分,第i项数组变成了无序,所以令right = i,继续遍历数组,重复以上操作。在同一个for循环内可以同时也实现从右往左的遍历,逻辑差不多,最后得到left和right后判断right是否大于left,不大于说明不需要改动,输出0,大于则输出right - left + 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
int findUnsortedSubarray(vector<int>& nums) {
if(nums.size() <= 1)
return 0;
int len = nums.size(), low = 0, high = len -1, maxNum = nums[0], minNum = nums[len-1];
for(int i = 1; i < len; i++){
maxNum = max(maxNum, nums[i]);
minNum = min(minNum, nums[len - 1 - i]);
if(nums[i] < maxNum)
low = i;
if(nums[len - 1 - i] > minNum)
high = len - 1 -i;
}
return low > high ? low - high + 1 : 0;
}
};
|
605 种花问题
605. 种花问题 - 力扣(LeetCode)
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false 。
示例 1:
输入:flowerbed = [1,0,0,0,1], n = 1
输出:true
示例 2:
输入:flowerbed = [1,0,0,0,1], n = 2
输出:false
题解:
防御式编程思想:在 flowerbed 数组两端各增加一个 0, 这样处理的好处在于不用考虑边界条件,任意位置处只要连续出现三个 0 就可以栽上一棵花。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
int len = 1, ans = 0; //认为左边界提供1个0
for (auto &i : flowerbed) {
if (i) {//为1,遇到1了
ans += (len - 1) / 2; //len个0可以种这么多花
len = 0;
}
else {//为0
++len;
}
}
ans += (len) / 2; //处理0尾,认为右边界提供一个0
return ans >= n;
}
};
|
628 三个数的最大乘积
628. 三个数的最大乘积 - 力扣(LeetCode)
给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。
示例 1:
输入:nums = [1,2,3]
输出:6
示例 2:
输入:nums = [1,2,3,4]
输出:24
示例 3:
输入:nums = [-1,-2,-3]
输出:-6
题解:
创建五个变量分别存储最大值、第二大值、第三大值、最小值、第二小值
① 若thirdMax > 0,毫无疑问最大的结果为firstMax * secondMax * thirdMax
② 若只有thirdMax <= 0,则上述结果不一定最大,可与firstMin * secondMin * firstMax比较
③ 若只有firstMax > 0,则上述两个结果也无法确定,可计算出结果比较
综上,我们可以将两个结果算出来直接选最大的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public:
int maximumProduct(vector<int>& nums) {
int min1= INT_MAX, min2 = INT_MAX;
int max1 = INT_MIN, max2 = INT_MIN, max3 = INT_MIN;
for(int x : nums){
if(x < min1){
min2 = min1;
min1 = x;
}
else if(x < min2)
min2 = x;
if(x > max1){
max3 = max2;
max2 = max1;
max1 =x;
}
else if(x > max2){
max3 = max2;
max2 = x;
}
else if(x > max3)
max3 = x;
}
return max(min1*min2*max1, max1*max2*max3);
}
};
|
643 子数组最大平均数I
643. 子数组最大平均数 I - 力扣(LeetCode)
给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。
请你找出平均数最大且 长度为 k 的连续子数组,并输出该最大平均数。
任何误差小于 10-5 的答案都将被视为正确答案。
示例 1:
输入:nums = [1,12,-5,-6,50,3], k = 4
输出:12.75
解释:最大平均数 (12-5-6+50)/4 = 51/4 = 12.75
示例 2:
输入:nums = [5], k = 1
输出:5.00000
题解:
创建一个变量max用来保存长度为K的连续子数组的元素的和的最大值,然后一直遍历就OK了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
double findMaxAverage(vector<int>& nums, int k) {
int sum=0, i=0;
int n = nums.size();
for(i = 0; i < k; i++){
sum += nums[i];
}
int maxSum = sum;
for(i = k; i < n; i++){
sum = sum + nums[i] - nums[i-k];
maxSum = max(maxSum, sum);
}
return static_cast<double>(maxSum)/k;
}
};
|
665 非递减数列
665. 非递减数列 - 力扣(LeetCode)
给你一个长度为 n 的整数数组 nums ,请你判断在 最多 改变 1 个元素的情况下,该数组能否变成一个非递减数列。
我们是这样定义一个非递减数列的: 对于数组中任意的 i (0 <= i <= n-2),总满足 nums[i] <= nums[i + 1]。
示例 1:
输入: nums = [4,2,3]
输出: true
解释: 你可以通过把第一个 4 变成 1 来使得它成为一个非递减数列。
示例 2:
输入: nums = [4,2,1]
输出: false
解释: 你不能在只改变一个元素的情况下将其变为非递减数列。
题解:
假设一个数组有两对nums[i] > nums[i + 1],那这样结果一定为false
例如:[3, 2, 1]、[4, 2, 1, 3]
假设一个数组只有一堆nums[i] > nums[i + 1],结果也不一定为true
例如:[3, 4, 1, 2]
创建一个计数器cnt来存有几对
可见修改值之后还得再判断是否是非递减数列,但是老是遍历判断太费时间了,那还可以咋做呢?
假设现在nums[i] > nums[i + 1],则有两种改法,nums[i] = nums[i + 1]或者nums[i + 1] = nums[i]
对于前者,改完必须还要保证nums[i] >= nums[i - 1],既nums[i + 1] >= nums[i - 1],要不然就只能改nums[i + 1],
而对于前者改完我们也判断不到了,不影响整体判断,因为for循环i++,i已经到后面去了,所以我们不用处理前面的情况,只要处理一下改nums[i + 1]的情况,毕竟改完了我们还会遍历到i+1这个元素,看看改之后符不符合要求。在每次cnt++之后看看是否大于1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
bool checkPossibility(vector<int>& nums) {
int n = nums.size(), cnt = 0;
for(int i = 0; i < n-1; i++){
int x = nums[i], y = nums[i + 1];
if(x > y){
cnt++;
if(cnt > 1){
return false;
}
if(i > 0 && y < nums[i -1]){
nums[i + 1] = x;
}
}
}
return true;
}
};
|
674 最长连续递增序列
674. 最长连续递增序列 - 力扣(LeetCode)
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。
题解:
遍历,把符合条件的子数组长度求出来取最大值就OK
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int l = 0, r = 0, n = nums.size(), maxSize = 1, maxNum = INT_MIN;
for(int i = 0; i < n ; i++){
r = i;
if(maxNum >= nums[i]){
maxSize = max(maxSize, r - l);
l = r;
}
maxNum = nums[i];
}
maxSize = max(maxSize, r - l + 1 );
return maxSize;
}
};
|
697 数组的度
697. 数组的度 - 力扣(LeetCode)
给定一个非空且只包含非负数的整数数组 nums,数组的 度 的定义是指数组里任一元素出现频数的最大值。
你的任务是在 nums 中找到与 nums 拥有相同大小的度的最短连续子数组,返回其长度。
示例 1:
输入:nums = [1,2,2,3,1]
输出:2
解释:
输入数组的度是 2 ,因为元素 1 和 2 的出现频数最大,均为 2 。
连续子数组里面拥有相同度的有如下所示:
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
最短连续子数组 [2, 2] 的长度为 2 ,所以返回 2 。
示例 2:
输入:nums = [1,2,2,3,1,4,2]
输出:6
解释:
数组的度是 3 ,因为元素 2 重复出现 3 次。
所以 [2,2,3,1,4,2] 是最短子数组,因此返回 6 。
题解:
哈希表,存储每个值出现的次数、第一次出现的位置、最后一次出现的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public:
int findShortestSubArray(vector<int>& nums) {
unordered_map<int, vector<int >> mp;
int n = nums.size();
for(int i = 0; i < n; i++){
if(mp.count(nums[i])){
mp[nums[i]][0]++;
mp[nums[i]][2] = i;
}
else{
mp[nums[i]] = {1, i, i};
}
}
int maxNum = 0, minLen = 0;
for(auto&[_, vec] : mp){
if(maxNum < vec[0]){
maxNum = vec[0];
minLen = vec[2] - vec[1] + 1;
}
else if(maxNum == vec[0]){
if(minLen > vec[2] - vec[1] + 1){
minLen = vec[2] - vec[1] + 1;
}
}
}
return minLen;
}
};
|
717 1比特与2比特字符
717. 1 比特与 2 比特字符 - 力扣(LeetCode)
有两种特殊字符:
- 第一种字符可以用一比特
0 表示
- 第二种字符可以用两比特(
10 或 11)表示
给你一个以 0 结尾的二进制数组 bits ,如果最后一个字符必须是一个一比特字符,则返回 true 。
示例 1:
输入: bits = [1, 0, 0]
输出: true
解释: 唯一的解码方式是将其解析为一个两比特字符和一个一比特字符。
所以最后一个字符是一比特字符。
示例 2:
输入:bits = [1,1,1,0]
输出:false
解释:唯一的解码方式是将其解析为两比特字符和两比特字符。
所以最后一个字符不是一比特字符。
题解:
已知结尾一定是0,则可以从后面入手,找到结尾前一个0的位置,假设其位置分别为n,i(n为结尾),则这两个0中间一定有n - i - 2个1,判断是不是偶数就可以得到结果,因为n-i-2和n-i奇偶性相同,所以判断n-i是不是偶数即可
1
2
3
4
5
6
7
8
9
10
|
class Solution {
public:
bool isOneBitCharacter(vector<int> &bits) {
int n = bits.size(), i = n - 2;
while (i >= 0 and bits[i]) {
--i;
}
return (n - i) % 2 == 0;
}
};
|
724 寻找数组的中心下标
724. 寻找数组的中心下标 - 力扣(LeetCode)
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
输入:nums = [1, 7, 3, 6, 5, 6]
输出:3
解释:
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
输入:nums = [1, 2, 3]
输出:-1
解释:
数组中不存在满足此条件的中心下标。
示例 3:
输入:nums = [2, 1, -1]
输出:0
解释:
中心下标是 0 。
左侧数之和 sum = 0 ,(下标 0 左侧不存在元素),
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
题解:
因为左右两边相等,假设左边和为n,则2n+nums[i] = nums总和,求出数组所有元素和放在sum中,遍历数组,直到2×temp = 2×(nums[0] + … + nums[i-1]) = 2n - nums[i]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int sum = accumulate(nums.begin(), nums.end(), 0);
int temp = 0;
for (int i = 0; i < nums.size(); i++){
if(temp * 2 == sum - nums[i]){
return i;
}
temp += nums[i];
}
return -1;
}
};
|
747 至少是其他数字两倍的最大数
747. 至少是其他数字两倍的最大数 - 力扣(LeetCode)
给你一个整数数组 nums ,其中总是存在 唯一的 一个最大整数 。
请你找出数组中的最大元素并检查它是否 至少是数组中每个其他数字的两倍 。如果是,则返回 最大元素的下标 ,否则返回 -1 。
示例 1:
输入:nums = [3,6,1,0]
输出:1
解释:6 是最大的整数,对于数组中的其他整数,6 至少是数组中其他元素的两倍。6 的下标是 1 ,所以返回 1 。
示例 2:
输入:nums = [1,2,3,4]
输出:-1
解释:4 没有超过 3 的两倍大,所以返回 -1 。
题解:
没啥好说的,遍历找到最大和次大,判断是否两倍关系
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public:
int dominantIndex(vector<int>& nums) {
int maxNum = INT_MIN, lastMax = INT_MIN;
int sub = 0;
for (int i = 0; i < nums.size(); i++){
if (maxNum < nums[i]){
lastMax = maxNum;
maxNum = nums[i];
sub = i;
}
else if (lastMax < nums[i]){
lastMax = nums[i];
}
}
return maxNum >= 2 * lastMax ? sub : -1;
}
};
|
2 两数相加
2. 两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
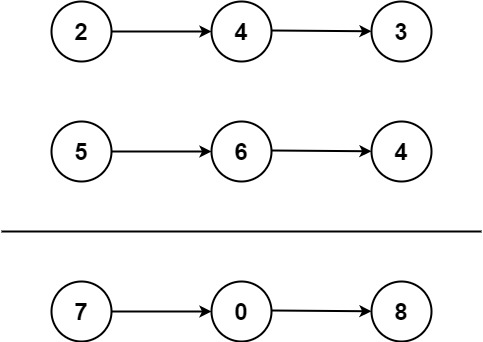
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
提示:
- 每个链表中的节点数在范围
[1, 100] 内
0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
题解:
第一版直接暴力求解,把链表的数字表示出来,溢出了😭😭😭
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
if (l1 == nullptr || l2 == nullptr)
return nullptr;
int num1 = 0, num2 = 0;
int d = 0;
//求l1的数值
if (l1->val != 0){
while (l1 != nullptr) {
num1 += l1->val * pow(10, d++);
l1 = l1->next;
}
}
//求l2的数值
d = 0;
if (l2->val != 0){
while (l2 != nullptr) {
num2 += l2->val * pow(10, d++);
l2 = l2->next;
}
}
//求结果
ListNode *pre = new ListNode(0);
int sum = num1 + num2;
ListNode *cur = pre;
while (sum > 0) {
ListNode *next = new ListNode(sum % 10);
cur->next = next;
cur = cur->next;
sum /= 10;
}
return pre->next == nullptr ? pre : pre->next;
}
};
|
执行出错
Line 27: Char 22: runtime error: 1e+10 is outside the range of representable values of type ‘int’ (solution.cpp) SUMMARY: UndefinedBehaviorSanitizer: undefined-behavior prog_joined.cpp:36:22
最后执行的输入
l1 =[9]
l2 =[1,9,9,9,9,9,9,9,9,9]
第二版看了题解,妙啊,对于按位运算可以这样做:将进位(carry)和求和(sum)分开考虑,sum每次加上两个数和进位,然后判断是否大于10,大于则sum %10,最后一位加完若进位存在,则最高位在添个1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
if (l1 == nullptr || l2 == nullptr)
return nullptr;
ListNode *pre = new ListNode(0);
int carry = 0; //进位
ListNode *cur = pre;
while (l1 != nullptr || l2 != nullptr) {
//每一位求和
int x = l1 == nullptr ? 0 : l1->val;
int y = l2 == nullptr ? 0 : l2->val;
int sum = x + y + carry;
carry = sum / 10; //求进位
sum %= 10; //sum一定小于10
cur->next = new ListNode(sum);
cur = cur->next;
if (l1 != nullptr)
l1 = l1->next;
if (l2 != nullptr)
l2 = l2->next;
}
if (carry > 0)
cur->next = new ListNode(carry);
return pre->next;
}
};
|
每日一题 2024/4/1
故障键盘
你的笔记本键盘存在故障,每当你在上面输入字符 'i' 时,它会反转你所写的字符串。而输入其他字符则可以正常工作。
给你一个下标从 0 开始的字符串 s ,请你用故障键盘依次输入每个字符。
返回最终笔记本屏幕上输出的字符串。
示例 1:
输入:s = "string"
输出:"rtsng"
解释:
输入第 1 个字符后,屏幕上的文本是:"s" 。
输入第 2 个字符后,屏幕上的文本是:"st" 。
输入第 3 个字符后,屏幕上的文本是:"str" 。
因为第 4 个字符是 'i' ,屏幕上的文本被反转,变成 "rts" 。
输入第 5 个字符后,屏幕上的文本是:"rtsn" 。
输入第 6 个字符后,屏幕上的文本是: "rtsng" 。
因此,返回 "rtsng" 。
示例 2:
输入:s = "poiinter"
输出:"ponter"
解释:
输入第 1 个字符后,屏幕上的文本是:"p" 。
输入第 2 个字符后,屏幕上的文本是:"po" 。
因为第 3 个字符是 'i' ,屏幕上的文本被反转,变成 "op" 。
因为第 4 个字符是 'i' ,屏幕上的文本被反转,变成 "po" 。
输入第 5 个字符后,屏幕上的文本是:"pon" 。
输入第 6 个字符后,屏幕上的文本是:"pont" 。
输入第 7 个字符后,屏幕上的文本是:"ponte" 。
输入第 8 个字符后,屏幕上的文本是:"ponter" 。
因此,返回 "ponter" 。
提示:
1 <= s.length <= 100s 由小写英文字母组成s[0] != 'i'
题解:
用双端队列反向模拟
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
string finalString(string s) {
deque<char> q;
bool back = false;
for (auto ch : s) {
if (ch != 'i') {
if (back)
q.push_back(ch);
else
q.push_front(ch);
}
else
back = !back;
}
string res = (back ? string{q.begin(), q.end()} : string{q.rbegin(), q.rend()});
return res;
}
};
|
5 最长回文子串
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
提示:
1 <= s.length <= 1000s 仅由数字和英文字母组成
题解:
动态规划,得多练练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution {
public:
string longestPalindrome(string s) {
if (s.size() == 0)
return "";
int start = 0, end = 0;
for (int i = 0; i < s.size(); i++) {
auto [left1, right1] = expandAroundCenter(s, i, i);
auto [left2, right2] = expandAroundCenter(s, i, i + 1);
if (right1 - left1 > end - start){
start = left1;
end = right1;
}
if (right2 - left2 > end - start) {
start = left2;
end = right2;
}
}
return s.substr(start, end - start + 1);
}
pair<int, int>expandAroundCenter(string &s, int i, int j){
int left = i, right = j;
while (left >= 0 && right <= s.size() && s[left] == s[right]) {
left--;
right++;
}
return {left + 1, right - 1};
}
};
|
每日一题 2024/4/2
所有可能的真二叉树
给你一个整数 n ,请你找出所有可能含 n 个节点的 真二叉树 ,并以列表形式返回。答案中每棵树的每个节点都必须符合 Node.val == 0 。
答案的每个元素都是一棵真二叉树的根节点。你可以按 任意顺序 返回最终的真二叉树列表**。**
真二叉树 是一类二叉树,树中每个节点恰好有 0 或 2 个子节点。
示例 1:
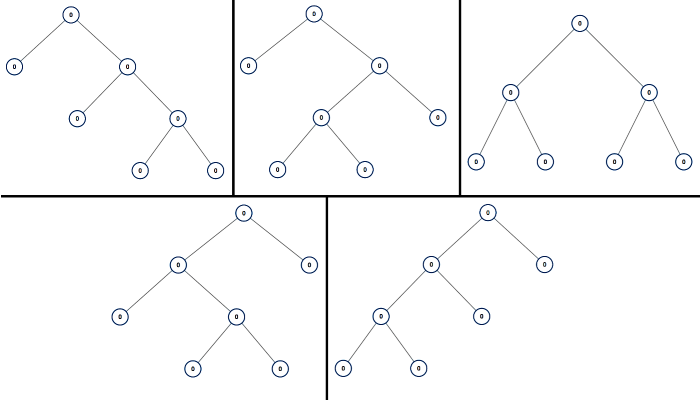
输入:n = 7
输出:[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
示例 2:
输入:n = 3
输出:[[0,0,0]]
提示:
题解:
分治思想,左右子树节点为i, n - 1 - i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
vector<TreeNode*> allPossibleFBT(int n) {
vector<TreeNode *> res;
if (n % 2 == 0)
return res;
if (n == 1){
res = {new TreeNode(0)};
return res;
}
for (int i = 1; i < n; i++) {
vector<TreeNode *> leftTree = allPossibleFBT(i);
vector<TreeNode *> rightTree = allPossibleFBT(n - 1 - i);
for (auto a : leftTree){
for (auto b : rightTree) {
TreeNode *root = new TreeNode(0, a, b);
res.push_back(root);
}
}
}
return res;
}
};
|
HOT100
1 两数之和
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
题解:
这是梦开始的地方啊,还记得大一的时候就知道了这个网站,笑死了知道了但是一直没刷过,我记得三年前就刷了这道题,而且还是很懵逼的状态刷的,没记错的话应该是暴力解法,毕竟当时啥也不会还能做出什么花来啊,没办法,然后刷完这道题就给我劝退了😅😅😅只怪当初自己太菜啊,什么数据结构都没有学过。如今我已大三,重亲捡起来了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> mp;
for (int i = 0; i < nums.size(); ++i) {
auto it = mp.find(target-nums[i]);
if (it != mp.end()) {
return {it->second, i};
}
mp[nums[i]] = i;
}
return {};
}
};
|
49 字母异异位词分组
49. 字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
输入: strs = [""]
输出: [[""]]
示例 3:
输入: strs = ["a"]
输出: [["a"]]
提示:
1 <= strs.length <= 1040 <= strs[i].length <= 100strs[i] 仅包含小写字母
题解:
一开始没搞懂题目意思,还以为不同单词可能有重复的位置的字母,结果没有,
用哈希表,key为排序后的str中的每个string(唯一的)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
unordered_map<string, vector<string>> mp;
for (auto &s : strs) {
string key = s;
sort(key.begin(), key.end()); //对key排序
mp[key].emplace_back(s);
}
vector<vector<string>> res;
for (auto it = mp.begin(); it != mp.end(); ++it) {
res.emplace_back(it->second);
}
return res;
}
};
|
128 最长连续序列
128. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109
题解:
第一版,利用哈希表存储,key为数组中的元素(其实可以用set),根据key查找对应的key+1在不在哈希表中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
if (nums.size() == 0)
return 0;
map<int, int> mp;
for (auto a : nums)
mp[a]++;
int maxLen = 1;
int maxNum = 1;
for (auto it = mp.begin(); it != mp.end(); it++) {
if (mp.count(1+it->first))
maxNum++;
else{
maxLen = max(maxNum, maxLen);
maxNum = 1;
}
}
return maxLen;
}
};
|
283 移动零
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:
1 <= nums.length <= 104-231 <= nums[i] <= 231 - 1
**进阶:**你能尽量减少完成的操作次数吗?
题解:
笑死了,一开始想用erase删除0,然后尾插0,但是逻辑出了点问题,会导致遍历到后面插入的几个0的时候死循环😅😅
还是用双指针好,右指针遍历,左指针指向非零数序列尾,右指针只要找到非零数就交换左右指针的数
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int n = nums.size(), right = 0, left = 0;
while (right < n) {
if (nums[right]) {
swap(nums[left], nums[right]);
left++;
}
right++;
}
}
};
|
11 盛最多水的容器
11. 盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
**说明:**你不能倾斜容器。
示例 1:

输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
题解:
双指针,从左右两端开始往中间靠,每次扔掉“短板”并维护最大容量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int maxArea(vector<int>& height) {
int left = 0, right = height.size() - 1;
int maxRes = 0;
while (left < right) {
int h = height[left] <= height[right] ? height[left] : height[right];//不能在这里left++或right--,因为后面res计算用到了
int res = h * (right - left);
maxRes = max(maxRes, res);
height[left] <= height[right] ? left++ : right--;
}
return maxRes;
}
};
|
15 三数之和
15. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
题解:
已经是二刷了,不过还是得加深印象啊,也是双指针类似问题。
只需要两层遍历,第一层找基数,第二层找和为0 - 基数的两个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> res;
if (nums.size() < 3)
return res;
sort(nums.begin(), nums.end()); //排序很重要,根据排序判断大小呢得
int n = nums.size();
for (int first = 0; first < n; first++) {
if (first > 0 && nums[first] == nums[first - 1])
continue;
int third = n - 1;
int target = -nums[first];
for (int second = first + 1; second < n; second++){
if (second > first + 1 && nums[second] == nums[second - 1])
continue;
while (second < third && nums[second] + nums[third] > target)
third--;
if (second == third)
break;
if (nums[second] + nums[third] == target)
res.push_back({nums[first], nums[second], nums[third]});
}
}
return res;
}
};
|
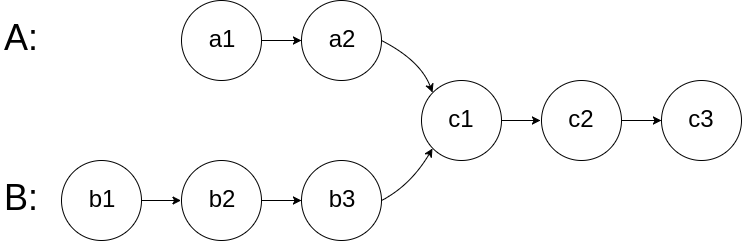
160 相交链表
160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交**:**
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal - 相交的起始节点的值。如果不存在相交节点,这一值为 0listA - 第一个链表listB - 第二个链表skipA - 在 listA 中(从头节点开始)跳到交叉节点的节点数skipB - 在 listB 中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
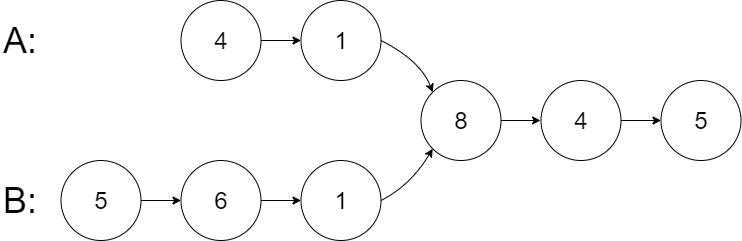
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
— 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
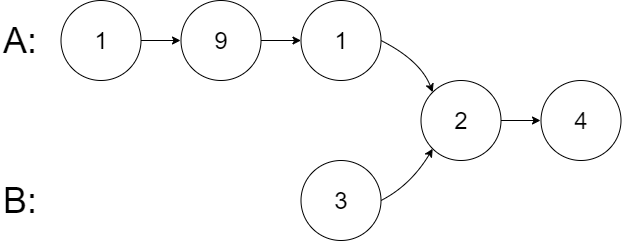
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
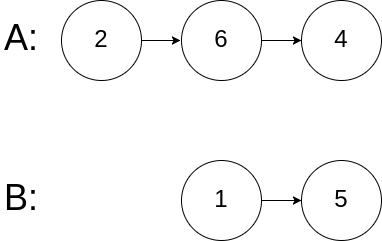
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA 中节点数目为 mlistB 中节点数目为 n1 <= m, n <= 3 * 1041 <= Node.val <= 1050 <= skipA <= m0 <= skipB <= n- 如果
listA 和 listB 没有交点,intersectVal 为 0
- 如果
listA 和 listB 有交点,intersectVal == listA[skipA] == listB[skipB]
**进阶:**你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案?
题解:
双指针,记住,不管有无交点,相交前的总和是一样的,无交点的情况可以看做交点为nullptr
1
2
3
4
5
6
7
8
9
10
11
|
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (!headA || !headB)
return nullptr;
ListNode *p1 = headA;
ListNode *p2 = headB;
while (p1 != p2) {
p1 = (p1 == nullptr ? headB : p1->next);
p2 = (p2 == nullptr ? headA : p2->next);
}
return p1;
}
|
42 接雨水
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
题解:
大名鼎鼎的接雨水,终于刷了哈,动态规划,第一版:(空间复杂度为O(n))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() == 0)
return 0;
int n = height.size() - 1;
vector<int> leftMax(height.size());
vector<int> rightMax(height.size());
leftMax[0] = height[0];
rightMax[n] = height[n];
for (int i = 1; i <= n; i++)
leftMax[i] = max(leftMax[i - 1], height[i]);
for (int i = n - 1; i >= 0; i--)
rightMax[i] = max(rightMax[i + 1], height[i]);
int ret = 0;
for (int i = 0; i <= n; i++)
ret += min(leftMax[i], rightMax[i]) - height[i];
return ret;
}
};
|
第二版,双指针,重要的就是理解,leftMax和rightMax。如果当前的数小于右边的数,则我这个点撑死了,最多接的水也就leftMax-本身,就算我这个点相邻好几个都是0,那也是左边那么多啊,因为右边大了呀
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() == 0)
return 0;
int left = 0, right = height.size() - 1;
int leftMax = 0, rightMax = 0;
int res = 0;
while (left < right) {
leftMax = max(leftMax, height[left]);
rightMax = max(rightMax, height[right]);
if (height[left] < height[right])
res += leftMax - height[left++];
else
res += rightMax - height[right--];
}
return res;
}
};
|
3 无重复字符的最长子串
3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的最长子串的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
提示:
0 <= s.length <= 5 * 104s 由英文字母、数字、符号和空格组成
题解:
滑动窗口,值得看看,感觉滑动窗口这方面挺欠缺
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
int lengthOfLongestSubstring(string s) {
if (s.size() == 0)
return 0;
unordered_set<char> st;
int r = -1;
int maxLen = 0;
for (int i = 0; i < s.size(); i++) {
if (i != 0)
st.erase(s[i - 1]);
while (r + 1 < s.size() && !st.count(s[r + 1])) {
st.insert(s[r + 1]);
r++; //右边可以滑,只要没有重复的
}
maxLen = max(maxLen, r - i + 1);
}
return maxLen;
}
|
438 找到字符串中所有字母异位词
438. 找到字符串中所有字母异位词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
示例 2:
输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
提示:
1 <= s.length, p.length <= 3 * 104s 和 p 仅包含小写字母
题解:
滑动窗口,妙啊,每次记录不相同的个数,然后根据这一个变量取舍就好了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
int slen = s.size(), plen = p.size();
if (slen < plen)
return vector<int> ();
vector<int> ans;
vector<int> count(26);
int differ = 0;
for (int i = 0; i < plen; i++) {
++count[s[i] - 'a'];
--count[p[i] - 'a'];
}
for (int i = 0; i < 26; i++) {
if (count[i] != 0)
++differ;
}
if (differ == 0)
ans.emplace_back(0);
for (int i = 0; i < slen - plen; i++) {
if (count[s[i] - 'a'] == 0) //当前字母s[i]的个数已经相同,结果往前滑又给他扔了,得,不同了
++differ;
else if (count[s[i] - 'a'] == 1) //当前字母s[i]个数不同,且差值为1,相当于多了1个,OK往前滑扔掉了,相同了
--differ;
--count[s[i] - 'a'];
//同理
if (count[s[i + plen] - 'a'] == 0)
++differ;
else if (count[s[i + plen] - 'a'] == -1)
--differ;
++count[s[i + plen] - 'a'];
if (differ == 0)
ans.emplace_back(i + 1);
}
return ans;
}
};
|
560 和为K的子数组
560. 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2
输出:2
示例 2:
输入:nums = [1,2,3], k = 3
输出:2
提示:
1 <= nums.length <= 2 * 104-1000 <= nums[i] <= 1000-107 <= k <= 107
题解:
一开始想用滑动窗口,不知道为什么不太好实现,看了看题解,用到了哈希表记录前缀和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int, int> mp;
mp[0] = 1;
int pre = 0, count = 0;
for (int a : nums) {
pre += a;
if (mp.find(pre - k) != mp.end())
count += mp[pre - k];
mp[pre]++;
}
return count;
}
};
|
239 滑动窗口最大值
239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
题解:
第一版,优先队列,不是最优,但是起码能解了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
if (n < k)
return vector<int> ();
priority_queue<pair<int, int>> que;
for (int i = 0; i < k; i++)
que.emplace(nums[i], i);
vector<int> ans = {que.top().first};
for (int i = k; i < n; i++) {
que.emplace(nums[i], i);
while (que.top().second <= i - k) {
que.pop();
}
ans.push_back(que.top().first);
}
return ans;
}
|
第二版,单调队列,时间复杂度和空间复杂度更低了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
int n = nums.size();
if (n < k)
return vector<int> ();
deque<int> q;
for (int i = 0; i < k; i++) {
while (!q.empty() && nums[i] >= nums[q.back()])
q.pop_back();
q.push_back(i);
}
vector<int> ans = {nums[q.front()]};
for (int i = k; i < n; i++) {
while (!q.empty() && nums[i] >= nums[q.back()])
q.pop_back();
q.push_back(i);
while (q.front() <= i - k) {
q.pop_front();
}
ans.push_back(nums[q.front()]);
}
return ans;
}
|
76 最小覆盖子串
76. 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
- 对于
t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
- 如果
s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
示例 2:
输入:s = "a", t = "a"
输出:"a"
解释:整个字符串 s 是最小覆盖子串。
示例 3:
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中,
因此没有符合条件的子字符串,返回空字符串。
提示:
m == s.lengthn == t.length1 <= m, n <= 105s 和 t 由英文字母组成
题解:
大致思虑就是滑动窗口,看看当前窗口中包含了t中的所有字符了吗?具体用哈希表实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
unordered_map<char, int> ori, cnt;
bool check() {
for (const auto &p : ori) {
if (cnt[p.first] < p.second)
return false;
}
return true;
}
string minWindow(string s, string t) {
int sLen = s.size(), tLen = t.size();
if (sLen < tLen)
return "";
int l = 0, r = -1;
int ansL = -1, len = INT_MAX;
for (const auto &c : t)
ori[c]++;
while (r < sLen) {
if (ori.find(s[++r]) != ori.end())
++cnt[s[r]];
while (check() && l <= r) {
if (r - l + 1 < len) {
len = r - l + 1;
ansL = l;
}
if (ori.find(s[l]) != ori.end())
--cnt[s[l]];
++l;
}
}
return ansL == -1 ? string() : s.substr(ansL, len);
}
|
53 最大子数组和
53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组
是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
**进阶:**如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
题解:
动态规划,理解理解,有兴趣可以尝试他说的分治
1
2
3
4
5
6
7
8
|
int maxSubArray(vector<int>& nums) {
int pre = 0, maxAns = nums[0];
for (const auto &a : nums) {
pre = max(pre + a, a);
maxAns = max(pre, maxAns);
}
return maxAns;
}
|
56 合并区间
56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
题解:
对区间左侧元素排序,然后就好求了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.size() == 0)
return {};
sort(intervals.begin(), intervals.end());
vector<vector<int>> merged;
for (int i = 0; i < intervals.size(); i++) {
int L = intervals[i][0], R = intervals[i][1];
if (!merged.size() || merged.back()[1] < L)
merged.push_back({L, R});
else
merged.back()[1] = max(merged.back()[1], R);
}
return merged;
}
|
189 轮转数组
189. 轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105
进阶:
- 尽可能想出更多的解决方案,至少有 三种 不同的方法可以解决这个问题。
- 你可以使用空间复杂度为
O(1) 的 原地 算法解决这个问题吗?
题解:
不会,看了题解,看的我一脸懵逼,数学上的理解,反复多看看吧
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
void rotate(vector<int>& nums, int k) {
int n = nums.size();
k = k % n;
int count = gcd(k, n);
for (int start = 0; start < count; ++start) {
int current = start;
int prev = nums[start];
do {
int next = (current + k) % n;
swap(nums[next], prev);
current = next;
} while (start != current);
}
}
|
238 除自身以外数组的乘积
238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 **不要使用除法,**且在 O(*n*) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
**进阶:**你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
题解:
解题思路:
本题的难点在于 不能使用除法 ,即需要 只用乘法 生成数组 ansansans 。根据题目对 ans[i]ans[i]ans[i] 的定义,可列出下图所示的表格。
根据表格的主对角线(全为 111 ),可将表格分为 上三角 和 下三角 两部分。分别迭代计算下三角和上三角两部分的乘积,即可 不使用除法 就获得结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
vector<int> productExceptSelf(vector<int>& nums) {
vector<int> ans(nums.size(), 1);
int n = nums.size();
if (n < 1)
return ans;
ans[0] = 1;
int temp = 1;
for (int i = 1; i < n; i++) {
ans[i] *= ans[i - 1] * nums[i - 1];
}
for (int i = n - 2; i >= 0; i--) {
temp *= nums[i + 1];
ans[i] *= temp;
}
return ans;
}
|
41 缺失的第一个正数
41. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
解释:范围 [1,2] 中的数字都在数组中。
示例 2:
输入:nums = [3,4,-1,1]
输出:2
解释:1 在数组中,但 2 没有。
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
解释:最小的正数 1 没有出现。
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 1
题解:
妙啊,利用原数组构造一个“哈希表”,重点就是理解一个长度为n的数组,最小未出现的整数只会在$[1,n+1]$的范围。为什么呢?因为只要数组元素任意一个大于n,则肯定有个漏了,且一定是在$[1,n+1]$的范围上,然后利用下标来当做这个判断条件,构造出只要出现过的就给对应值下标表示的元素设置成负数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
int firstMissingPositive(vector<int>& nums) {
if (nums.size() == 0)
return 0;
int n = nums.size();
/*先把负数全部改成n+1*/
for (int &num : nums) {
if (num <= 0)
num = n + 1;
}
/*标记过程*/
for (int i = 0; i < n; i++) {
int num = abs(nums[i]);
if (num <= n)
nums[num - 1] = -abs(nums[num - 1]);
}
/*根据标记判断*/
for (int i = 0; i < n; i++) {
if (nums[i] > 0)
return i + 1;
}
return n + 1;
}
|
73 矩阵置零
73. 矩阵置零
示例 1:
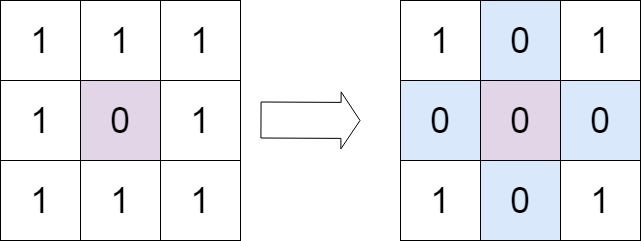
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
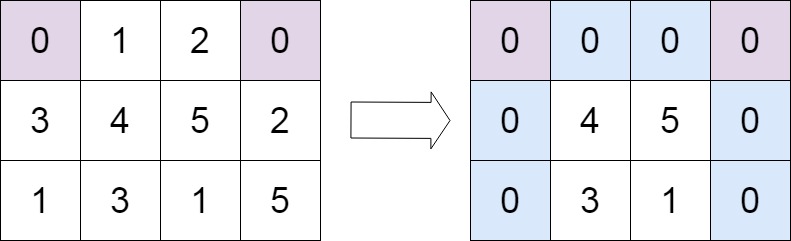
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
题解:
可以用辅助空间,用来表示某行某列是否需要置零,当然了官方题解给出了其他回答,可以看看(不过好像可读性不好)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
void setZeroes(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
vector<bool> rows(m), cols(n);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0)
rows[i] = cols[j] = true;
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (rows[i] || cols[j])
matrix[i][j] = 0;
}
}
}
|
54 螺旋矩阵
54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
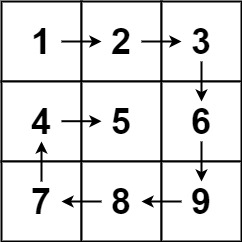
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
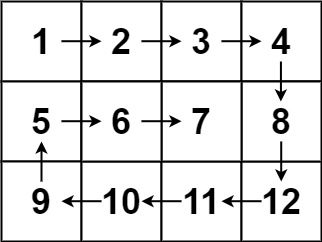
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
题解:
- 首先设定上下左右边界
- 其次向右移动到最右,此时第一行因为已经使用过了,可以将其从图中删去,体现在代码中就是重新定义上边界
- 判断若重新定义后,上下边界交错,表明螺旋矩阵遍历结束,跳出循环,返回答案
- 若上下边界不交错,则遍历还未结束,接着向下向左向上移动,操作过程与第一,二步同理
- 不断循环以上步骤,直到某两条边界交错,跳出循环,返回答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> ans;
if (matrix.empty()) return ans;
int u = 0;
int d = matrix.size() - 1;
int l = 0;
int r = matrix[0].size() - 1;
while (true) {
for (int i = l; i <= r; i++) ans.push_back(matrix[u][i]);
if (++u > d) break;
for (int i = u; i <= d; i++) ans.push_back(matrix[i][r]);
if (--r < l) break;
for (int i = r; i >= l; i--) ans.push_back(matrix[d][i]);
if (--d < u) break;
for (int i = d; i >= u; i--) ans.push_back(matrix[i][l]);
if (++l > r) break;
}
return ans;
}
};
|
48 旋转图像
48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:

输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
题解:
找规律,有点意思了哈,和数学有关(让我想起了图形学)
1
2
3
4
5
6
7
8
9
10
11
12
13
|
void rotate(vector<vector<int>>& matrix) {
if (matrix.empty()) return;
int n = matrix.size();
for (int i = 0; i < n /2; ++i) {
for (int j = 0; j < (n + 1) / 2; ++j) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][i]; //这算是一个公式
matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
matrix[j][n - i - 1] = temp;
}
}
}
|
240 搜索二维矩阵II
240. 搜索二维矩阵 II
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
题解:
有意思了哈,从最右上方开始排除,如果小了说明这一行都小了,往下走,如果大了说明该位置所在的列往下都大了,往左走,知道找到或者越界了
1
2
3
4
5
6
7
8
9
10
11
12
13
|
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
int x = 0, y = n - 1;
while (x < m && y >= 0) {
if (matrix[x][y] == target)
return true;
else if (matrix[x][y] > target)
--y;
else
++x;
}
return false;
}
|
160 相交链表
160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交**:**
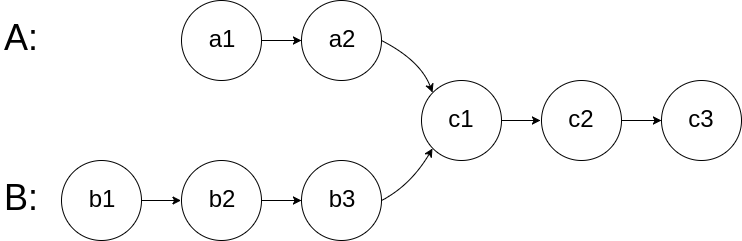
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal - 相交的起始节点的值。如果不存在相交节点,这一值为 0listA - 第一个链表listB - 第二个链表skipA - 在 listA 中(从头节点开始)跳到交叉节点的节点数skipB - 在 listB 中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
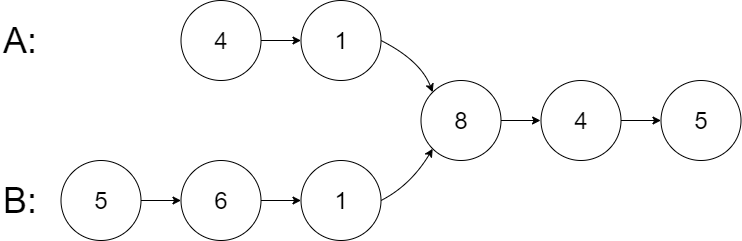
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
— 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
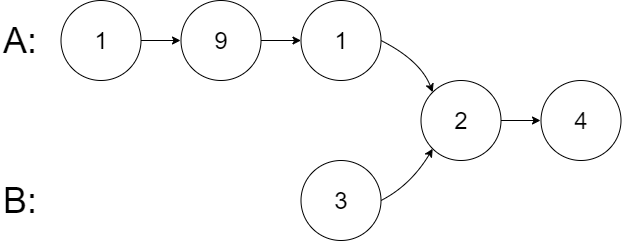
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
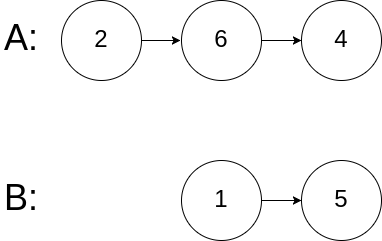
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
题解:
其实已经是很多次做这个题了,记住while循环里要判断的是节点本身是否为空,如果判断next则这辈子都出不去循环(不可能相等,我老是判断next)
1
2
3
4
5
6
7
8
9
10
11
|
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (headA == nullptr || headB == nullptr)
return nullptr;
ListNode *p1 = headA;
ListNode *p2 = headB;
while (p1 != p2) {
p1 = p1 ? p1->next : headB;
p2 = p2 ? p2->next : headA;
}
return p1;
}
|
206 反转链表
206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
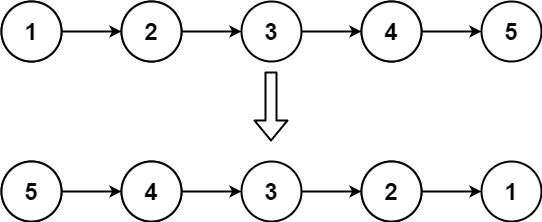
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
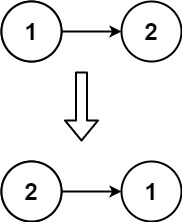
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
题解:
经典题目了,先来个前序节点就OK
1
2
3
4
5
6
7
8
9
10
11
12
13
|
ListNode* reverseList(ListNode* head) {
if (head == nullptr)
return nullptr;
ListNode *pre = nullptr;
ListNode *cur = head;
while (cur) {
ListNode *next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
|
234 回文链表
234. 回文链表
给你一个单链表的头节点 head ,请你判断该链表是否为
回文链表。如果是,返回 true ;否则,返回 false 。
示例 1:

输入:head = [1,2,2,1]
输出:true
示例 2:
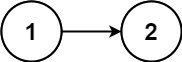
输入:head = [1,2]
输出:false
提示:
- 链表中节点数目在范围
[1, 105] 内
0 <= Node.val <= 9
**进阶:**你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
题解:
原地构造,使用快慢指针,将后面一般的节点逆序,然后两边一起遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
bool isPalindrome(ListNode* head) {
ListNode *fast = head;
ListNode *slow = head;
while (fast != nullptr && fast->next != nullptr) {
fast = fast->next->next;
slow = slow->next;
}
fast = head;
ListNode *pre = nullptr;
while (slow) {
ListNode *next = slow->next;
slow->next = pre;
pre = slow;
slow = next;
}
while (pre != nullptr && pre != fast) {
if (pre->val != fast->val)
return false;
pre = pre->next;
fast = fast->next;
}
return true;
}
|
141 环形链表
141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
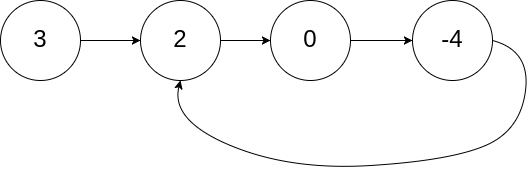
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
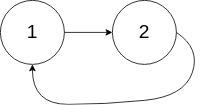
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
题解:
也是很经典的题了,双指针,快慢指针如果相遇的话一定有环,如果快指针会走空的话一定无环,不过有个小细节:程序开始判断一下单个元素和没有元素的情况,加快一丢丢时间
1
2
3
4
5
6
7
8
9
10
11
12
13
|
bool hasCycle(ListNode *head) {
if (head == nullptr || head->next == nullptr)
return false;
ListNode *fast = head;
ListNode *slow = head;
while (fast != nullptr && fast->next != nullptr) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow)
return true;
}
return false;
}
|
142 环形链表II
142. 环形链表 II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
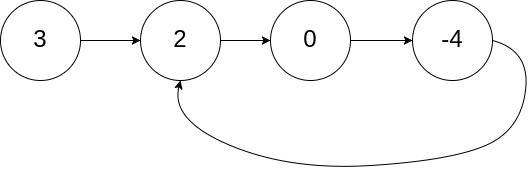
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
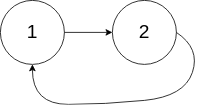
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
题解:
也是经典的题了,双指针很轻松解决,不过原理还是值得搞清楚一下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
ListNode *detectCycle(ListNode *head) {
if (head == nullptr || head->next == nullptr)
return nullptr;
ListNode *fast = head->next->next;
ListNode *slow = head->next;
while (fast != slow) {
if (fast == nullptr || fast->next == nullptr)
return nullptr;
fast = fast->next->next;
slow = slow->next;
}
fast = head;
while (fast != slow) {
fast = fast->next;
slow = slow->next;
}
return slow;
}
|
21 合并两个有序链表
21. 合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
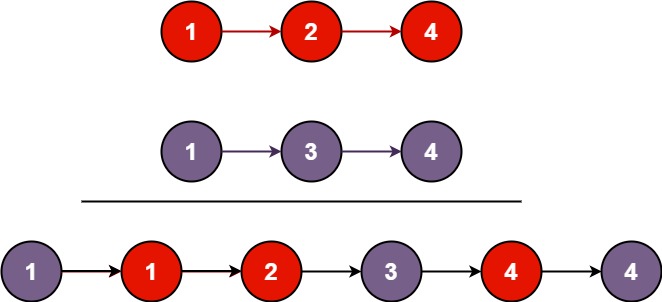
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
题解:
也是很经典的链表题目了,练熟(细节就是返回的一定是构造出来的“哨兵”的下一个节点)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
ListNode *pre = new ListNode(0);
ListNode *head = pre;
while (list1 != nullptr && list2 != nullptr) {
if (list1->val < list2->val) {
pre->next = list1;
list1 = list1->next;
}
else {
pre->next = list2;
list2 = list2->next;
}
pre = pre->next;
}
pre->next = list1 ? list1 : list2; //别忘记收尾
return head->next;
}
|
2 两数相加
2. 两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
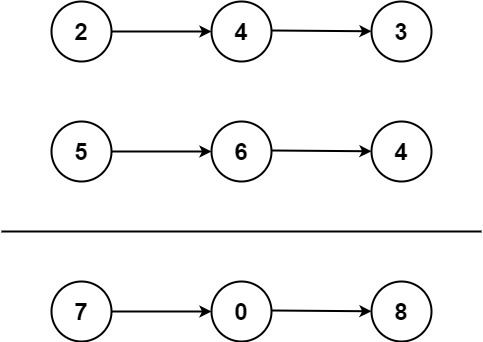
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
题解:
主要的一个问题是节点两个值会有进位的问题,处理好就可以了[^ note]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
if (l1 == nullptr || l2 == nullptr)
return nullptr;
int carry = 0, sum = 0;
ListNode *pre = new ListNode(0);
ListNode *cur = pre;
while (l1 != nullptr || l2 != nullptr) {
int x = l1 ? l1->val : 0;
int y = l2 ? l2->val : 0;
sum = x + y + carry;
carry = sum / 10;
sum = sum % 10;
cur->next = new ListNode(sum);
cur = cur->next;
if (l1) l1 = l1->next;
if (l2) l2 = l2->next;
}
if (carry)
cur->next = new ListNode(carry);
return pre->next;
}
|
19 删除链表的倒数第N个结点
19. 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
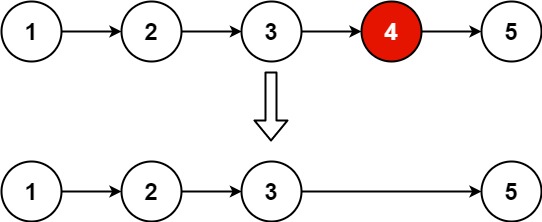
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
题解:
想法是没问题的,不过没Coding出来,再好好看看(一开始用了while循环,不太好搞啊)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
ListNode* removeNthFromEnd(ListNode* head, int n) {
int len = 0;
ListNode *cur = head;
ListNode *pre = new ListNode(0);
pre->next = cur;
while (cur != nullptr) {
++len;
cur = cur->next;
}
cur = pre;
int cnt = len - n + 1;
for (int i = 1; i < len - n + 1; ++i)
cur = cur->next;
cur->next = cur->next->next;
ListNode *ans = pre->next;
delete pre;
return ans;
}
|
24 两两交换链表中的节点
24. 两两交换链表中的节点
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
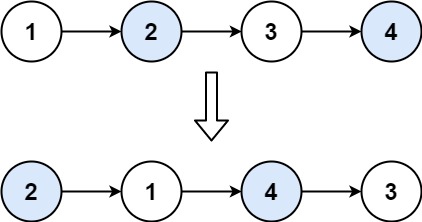
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
题解:
思路也没问题,不过又没Coding出来,注意好好利用pre指针,不要想着cur了容易出错呢
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
ListNode* swapPairs(ListNode* head) {
ListNode *newHead = new ListNode(0);
newHead->next = head;
ListNode *temp = newHead; //善用哨兵
while (temp->next && temp->next->next) {
ListNode *node1 = temp->next;
ListNode *node2 = temp->next->next;
temp->next = node2;
node1->next = node2->next;
node2->next = node1;
temp = node1;
}
ListNode *res = newHead->next;
delete newHead;
return res;
}
|
25 K个一组翻转链表
25. K 个一组翻转链表
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
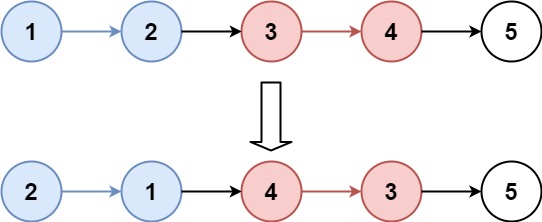
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
示例 2:
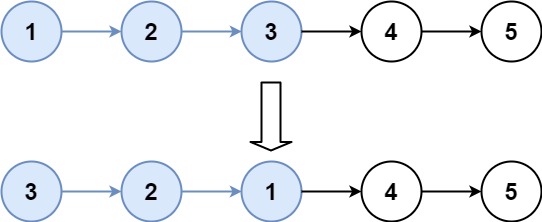
输入:head = [1,2,3,4,5], k = 3
输出:[3,2,1,4,5]
题解:
思路是没问题的,用一个处理函数返回处理后的头和尾,不过注意一下如何Coding
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
pair<ListNode*, ListNode*> myReverse(ListNode *head, ListNode *end) {
ListNode *pre = end->next;
ListNode *cur = head;
while (pre != end) {
ListNode *nex = cur->next;
cur->next = pre;
pre = cur;
cur = nex;
}
return {end, head};
}
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode *res = new ListNode(-1);
res->next = head;
ListNode *pre = res;
while (head) {
ListNode *end = pre;
for (int i = 0; i < k; ++i) {
end = end->next;
if (!end)
return res->next;
}
ListNode *nex = end->next;
pair<ListNode*, ListNode*> temp = myReverse(head, end);
head = temp.first, end = temp.second;
pre->next = head;
end->next = nex;
pre = end;
head = nex;
}
return res->next;
}
|
138 随机链表的复制
138. 随机链表的复制
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。
示例 1:
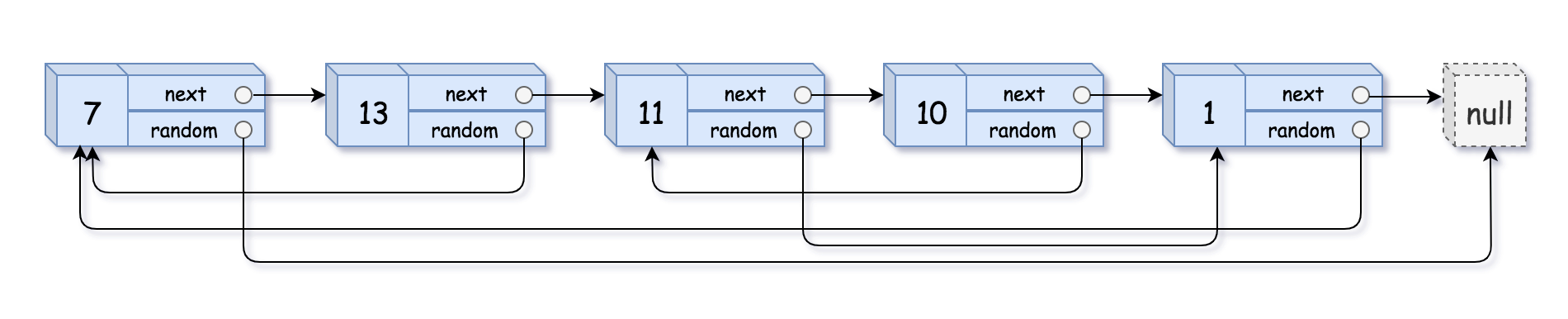
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:

输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例 3:

输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
题解:
这其实是第二次做这个题,还是有些不熟练啊
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
Node* copyRandomList(Node* head) {
if (head == nullptr)
return nullptr;
Node *cur = head;
Node *next = nullptr;
while (cur != nullptr) {
next = cur->next;
Node *copyNode = new Node(cur->val);
copyNode->next = next;
cur->next = copyNode;
cur = next;
}
Node *copyNode = nullptr;
cur = head;
while (cur != nullptr) {
next = cur->next->next;
copyNode = cur->next;
copyNode->random = (cur->random == nullptr) ? nullptr : cur->random->next;
cur = next;
}
Node *res = head->next;
cur = head;
while (cur != nullptr) {
next = cur->next->next;
copyNode = cur->next;
cur->next = next;
copyNode->next = (next == nullptr) ? nullptr : next->next;
cur = cur->next;
}
return res;
}
|
148 排序链表
148. 排序链表
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:
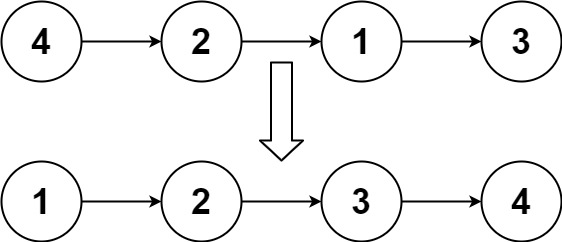
输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:
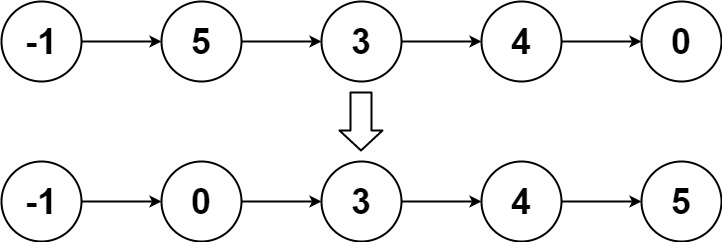
输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
示例 3:
输入:head = []
输出:[]
题解:
归并排序思想,记得对链表拆分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
ListNode* sortList(ListNode* head) {
if (head == nullptr)
return nullptr;
int length = 0;
ListNode *node = head;
while (node != nullptr) {
++length;
node = node->next;
}
ListNode *help = new ListNode(0, head);
for (int subLength = 1; subLength < length; subLength <<= 1) {
ListNode *pre = help, *cur = help->next;
while (cur != nullptr) {
ListNode *head1 = cur;
for(int i = 1; i < subLength && cur->next != nullptr; ++i)
cur = cur->next;
ListNode *head2 = cur->next;
cur->next = nullptr;
cur = head2;
for (int i = 1; i < subLength && cur != nullptr && cur->next != nullptr; ++i)
cur = cur->next;
ListNode *next = nullptr;
if (cur != nullptr) {
next = cur->next;
cur->next = nullptr;
}
ListNode *merged = merge(head1, head2);
pre->next = merged;
while (pre->next != nullptr)
pre = pre->next;
cur = next;
}
}
return help->next;
}
ListNode *merge(ListNode *head1, ListNode *head2) {
ListNode *newHead = new ListNode(0);
ListNode *temp = newHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
}
else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
temp->next = temp1 ? temp1 : temp2;
return newHead->next;
}
|
合并K个升序链表
23. 合并 K 个升序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
题解:
归并排序思想,把vector中的链表两两合并就OK(好好看看)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
ListNode* mergeKLists(vector<ListNode*>& lists) {
if (lists.size() == 0)
return nullptr;
return mergeSort(lists, 0, lists.size() - 1);
}
ListNode *mergeSort(vector<ListNode *> &lists, int l, int r) {
if (l > r)
return nullptr;
if (l == r)
return lists[l];
int mid = l + ((r - l) >> 1);
return merge(mergeSort(lists, l, mid), mergeSort(lists, mid + 1, r));
}
ListNode *merge(ListNode *node1, ListNode *node2) {
ListNode *pre = new ListNode(0);
ListNode *cur = pre;
while (node1 && node2) {
if (node1->val <= node2->val) {
cur->next = node1;
node1 = node1->next;
}
else {
cur->next = node2;
node2 = node2->next;
}
cur = cur->next;
}
if (node1)
cur->next = node1;
if (node2)
cur->next = node2;
return pre->next;
}
|
146 LRU缓存
146. LRU 缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
题解:
挺六的,题目要手搓一个双向链表并且用到了一个哈希map辅助查询
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
struct DLinkedNode { //双向链表(表头表示最近使用过,表尾为最近最久未使用)
int key, value;
DLinkedNode *prev;
DLinkedNode *next;
DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};
class LRUCache {
private:
unordered_map<int, DLinkedNode*> cache;
DLinkedNode* head;
DLinkedNode* tail;
int size;
int capacity;
public:
LRUCache(int _capacity): capacity(_capacity), size(0) {
head = new DLinkedNode();
tail = new DLinkedNode();
head->next = tail;
tail->prev = head;
}
int get(int key) {
if (!cache.count(key))
return -1;
DLinkedNode *node = cache[key];
moveToHead(node);
return node->value;
}
void put(int key, int value) {
if (!cache.count(key)) {
DLinkedNode *node = new DLinkedNode(key, value);
cache[key] = node;
addToHead(node);
++size;
if (size > capacity) {
DLinkedNode *removed = removeTail();
cache.erase(removed->key);
delete removed;
--size;
}
}
else {
DLinkedNode *node = cache[key];
node->value = value;
moveToHead(node);
}
}
void addToHead(DLinkedNode *node) {
node->prev = head;
node->next = head->next;
head->next->prev = node;
head->next = node;
}
void removeNode(DLinkedNode *node) {
node->prev->next = node->next;
node->next->prev = node->prev;
}
void moveToHead(DLinkedNode *node) {
removeNode(node);
addToHead(node);
}
DLinkedNode *removeTail() {
DLinkedNode *node = tail->prev;
removeNode(node);
return node;
}
};
|
543 二叉树的路径
543. 二叉树的直径
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
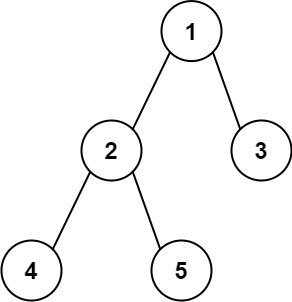
输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
输入:root = [1,2]
输出:1
题解:
其实就是套路的一个变体,向左右孩子要信息(最大的节点数,因为路劲=节点数-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
|
int maxRes = 1;
int diameterOfBinaryTree(TreeNode* root) {
depth(root);
return maxRes - 1;
}
int depth(TreeNode *root) {
if (root == nullptr)
return 0;
int l = depth(root->left);
int r = depth(root->right);
maxRes = max(maxRes, l + r + 1);
return max(l, r) + 1;
}
|
102 二叉树的层序遍历
102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
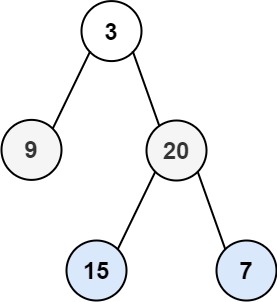
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
题解:
用到了队列来辅助完成
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
if (root == nullptr)
return ans;
queue<TreeNode*> q;
vector<int> help;
q.push(root);
while (!q.empty()) {
int temp = q.size();
for (int i = 0; i < temp; ++i) {
TreeNode *temp = q.front();
help.push_back(temp->val);
if (temp->left)
q.push(temp->left);
if (temp->right)
q.push(temp->right);
q.pop();
}
ans.push_back(help);
help.erase(help.begin(), help.end());
}
return ans;
}
|
108 将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡二叉搜索树。
示例 1:
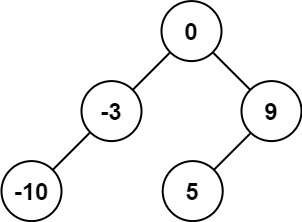
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
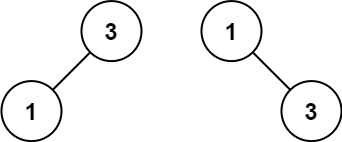
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
题解:
二叉树中序递归,思路得打开啊
1
2
3
4
5
6
7
8
9
10
11
12
13
|
TreeNode* sortedArrayToBST(vector<int>& nums) {
return buildTree(nums, 0, nums.size() - 1);
}
TreeNode *buildTree(vector<int> &nums, int l, int r) {
if (l > r)
return nullptr;
int mid = l + ((r - l) >> 1);
TreeNode *root = new TreeNode(nums[mid]);
root->left = buildTree(nums, l, mid - 1);
root->right = buildTree(nums, mid + 1, r);
return root;
}
|
98 验证二叉搜索树
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3]
输出:true
示例 2:
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
题解:
二叉树递归,主要就是看看判断逻辑怎么处理
1
2
3
4
5
6
7
8
9
10
|
bool helper(TreeNode *root, long long lower, long long upper) {
if (root == nullptr)
return true;
if (root->val <= lower || root->val >= upper)
return false;
return helper(root->left, lower, root->val) && helper(root->right, root->val, upper);
}
bool isValidBST(TreeNode* root) {
return helper(root, LONG_MIN, LONG_MAX);
}
|
98 验证二叉搜索树
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
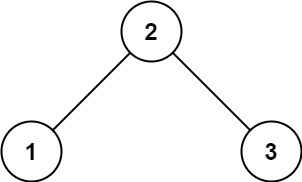
输入:root = [2,1,3]
输出:true
示例 2:
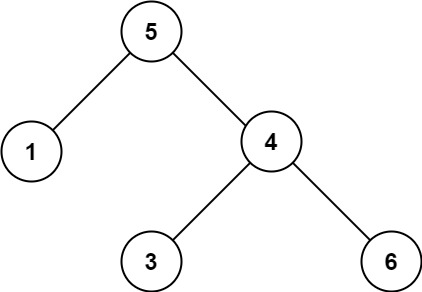
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
题解:
判断当前节点是否属于左右节点的值的区间范围内(开区间)即:$root→value\in(root→left→value,root→right→value) $,递归判断当前节点左右孩子是否满足,如果为空节点返回true
1
2
3
4
5
6
7
8
9
10
|
bool helper(TreeNode *root, long long lower, long long upper) {
if (root == nullptr)
return true;
if (root->val <= lower || root->val >= upper)
return false;
return helper(root->left, lower, root->val) && helper(root->right, root->val, upper);
}
bool isValidBST(TreeNode* root) {
return helper(root, LONG_MIN, LONG_MAX);
}
|
230 二叉搜索树中第K小的元素
230. 二叉搜索树中第K小的元素
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
示例 1:
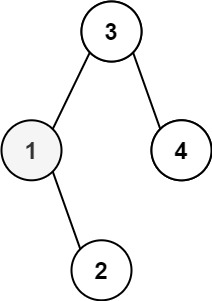
输入:root = [3,1,4,null,2], k = 1
输出:1
示例 2:
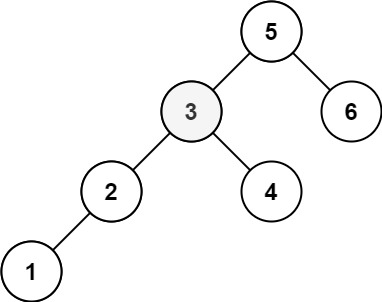
输入:root = [5,3,6,2,4,null,null,1], k = 3
输出:3
题解:
最简单的中序遍历递归方法:(当然有更优解法,不过有兴趣再看看吧)
1
2
3
4
5
6
7
8
9
10
11
|
int cnt = 0;
int kthSmallest(TreeNode* root, int k) {
if (root == nullptr)
return 0;
int leftval = kthSmallest(root->left, k);
++cnt;
if (cnt == k)
return root->val;
int rightval = kthSmallest(root->right, k);
return leftval ? leftval : rightval;
}
|
199 二叉树的右视图
199. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
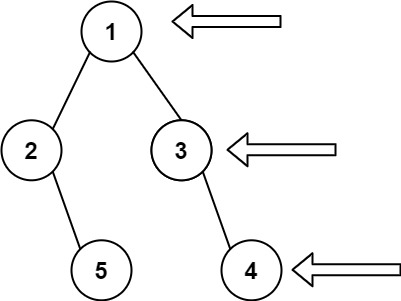
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
示例 2:
输入: [1,null,3]
输出: [1,3]
示例 3:
输入: []
输出: []
题解:
用一个队列实现层序遍历,可以再考虑考虑用常数实现,到时候去看看之前看过的一个视频
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
vector<int> rightSideView(TreeNode* root) {
vector<int> ans;
if (root == nullptr)
return ans;
queue<TreeNode*> que;
que.push(root);
while (!que.empty()) {
int temp = que.size();
while (true) {
TreeNode *cur = que.front();
que.pop();
--temp;
if (cur->left) que.push(cur->left);
if (cur->right) que.push(cur->right);
if (temp == 0) {
ans.push_back(cur->val);
break;
}
}
}
return ans;
}
|
114 二叉树展开为链表
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
- 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:

输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [0]
输出:[0]
题解:
很帅,中心思想就是把当前节点的右节点接到左子树最右边的节点的右节点后面
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
void flatten(TreeNode* root) {
TreeNode *cur = root;
while (cur != nullptr) {
if (cur->left != nullptr) {
TreeNode *save = cur->left;
TreeNode *pre = save;
while (pre->right != nullptr)
pre = pre->right;
pre->right = cur->right;
cur->left = nullptr;
cur->right = save;
}
cur = cur->right;
}
}
|
105 从前序与中序遍历序列构造二叉树
105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
题解:
老题了,好好看看
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
TreeNode *root = buildTree(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1);
return root;
}
TreeNode *buildTree(vector<int> &preorder, int l1, int r1, vector<int> &inorder, int l2, int r2) {
if (l1 > r1 || l2 > r2)
return nullptr;
TreeNode *root = new TreeNode(preorder[l1]);
int index = l2;
while (index <= r2) {
if (preorder[l1] == inorder[index])
break;
++index;
}
int nodes = index - l2;
root->left = buildTree(preorder, l1 + 1, l1 + nodes, inorder, l2, index - 1);
root->right = buildTree(preorder, l1 + nodes + 1, r1, inorder, index + 1, r2);
return root;
}
|
437 路径总和
437. 路径总和 III
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:

输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:3
题解:
第二次做这个题了,第一次是在牛客的剑指Offer,主要就用到了map保存前缀和来避免多余的重复计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
unordered_map<long long, int> map;
int pathSum(TreeNode* root, int targetSum) {
map[0] = 1;
return findPath(root, targetSum, 0);
}
int findPath(TreeNode *root, int targetSum, long long last)
{
if (root == nullptr)
return 0;
int res = 0;
last += root->val;
if (map.find(last - targetSum) != map.end()) {
res = map[last - targetSum];
}
++map[last];
res += findPath(root->left, targetSum, last);
res += findPath(root->right, targetSum, last);
--map[last];
return res;
}
|
236 二叉树的最近公共祖先
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
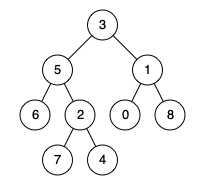
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
题解:
好几次做这个题了,重点就是二叉树dp,向左右子树要信息(有没有p或者q)
1
2
3
4
5
6
7
8
9
|
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == nullptr || root == p || root == q)
return root;
TreeNode *leftdata = lowestCommonAncestor(root->left, p, q);
TreeNode *rightdata = lowestCommonAncestor(root->right, p, q);
if (leftdata && rightdata)
return root;
return leftdata ? leftdata : rightdata;
}
|
124 二叉树中的最大路径和
124. 二叉树中的最大路径和
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
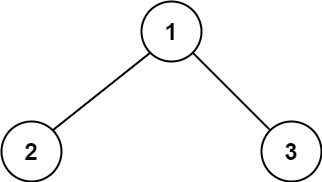
输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
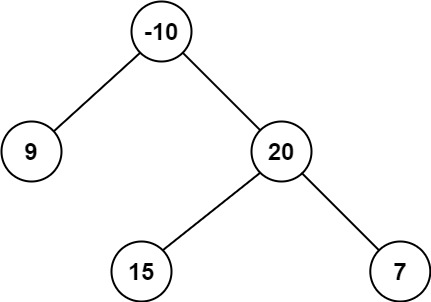
输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
题解:
其实还是树形DP,向左右子树要信息(左右能提供的最大和),然后加上自身,得到经过当前节点的一条最大路径和,维护一下maxSum
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int maxSum = INT_MIN;
int maxPathSum(TreeNode* root) {
help(root);
return maxSum;
}
int help(TreeNode *root) {
if (root == nullptr)
return 0;
int leftData = max(help(root->left), 0);
int rightData = max(help(root->right), 0);
int temp = root->val + leftData + rightData;
maxSum = max(temp, maxSum);
return root->val + max(leftData, rightData);
}
|
200 岛屿数量
200. 岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
题解:
看了题解区大佬的精华题解,妙啊,学到了,图的dfs套路和二叉树的挺像
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
void dfs(vector<vector<char>> &grid, int x, int y) {
if (!inGrid(grid, x, y)) //base case
return;
if (grid[x][y] == '1') { //递归
grid[x][y] = '2';
dfs(grid, x - 1, y);
dfs(grid, x + 1, y);
dfs(grid, x, y - 1);
dfs(grid, x, y + 1);
}
}
int numIslands(vector<vector<char>>& grid) {
int ans = 0;
int n = grid.size();
int m = grid[0].size();
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (grid[i][j] == '1') {
++ans;
dfs(grid, i, j);
}
}
}
return ans;
}
bool inGrid(vector<vector<char>> &grid, int x, int y) {
int m = grid.size();
int n = grid[0].size();
if (x < 0 || y < 0 || x >= m || y >= n)
return false;
return true;
}
|
994 腐烂的橘子
994. 腐烂的橘子
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值
0 代表空单元格;
- 值
1 代表新鲜橘子;
- 值
2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
示例 1:
输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:grid = [[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个方向上。
示例 3:
输入:grid = [[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
题解:
大概意思就是广度优先搜索,首先用一个辅助数组记录一下每个橘子腐烂时间,一开始把所有设置为-1,然后遍历一遍矩阵,如果遇到腐烂的句子就把相应位置的腐烂时间设置为0(这个才是初始值,其实用-1为了区分腐烂区和新鲜区),并将该位置加入队列(用于广度优先搜索),最后队列非空就一直搜索下去,只要记录的新鲜橘子数大于0则返回-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
int badTime[10][10];
int cnt = 0;
int dir_x[4] = {0, 0, 1, -1}; //行
int dir_y[4] = {1, -1, 0, 0}; //列
int orangesRotting(vector<vector<int>>& grid) {
int m = grid.size(); //行
int n = grid[0].size(); //列
memset(badTime, -1, sizeof(badTime));
queue<pair<int, int>> badOranges;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 2) {
badOranges.emplace(i, j);
badTime[i][j] = 0;
}
else if (grid[i][j] == 1) {
++cnt;
}
}
}
int ans = 0;
while (!badOranges.empty()) {
auto [row, col] = badOranges.front();
badOranges.pop();
for (int i = 0; i < 4; ++i) {
int dx = row + dir_x[i];
int dy = col + dir_y[i];
if (dx < 0 || dy < 0 || dx >= m || dy >= n ||
badTime[dx][dy] != -1 || grid[dx][dy] == 0)
continue;
badTime[dx][dy] = badTime[row][col] + 1;
badOranges.emplace(dx, dy);
if (grid[dx][dy] == 1) {
--cnt;
ans = badTime[dx][dy];
if (cnt == 0) break;
}
}
}
return cnt == 0 ? ans : -1;
}
|
46 全排列
46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
题解:
递归回溯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> ans;
if (nums.size() == 0)
return ans;
sort(nums.begin(), nums.end());
findAns(nums, ans, 0);
return ans;
}
void findAns(vector<int> &nums, vector<vector<int>> &ans, int index) {
if (index == nums.size())
ans.push_back(nums);
for (int i = index; i < nums.size(); ++i) {
swap(nums[i], nums[index]);
findAns(nums, ans, index + 1);
swap(nums[i], nums[index]);
}
}
|
35 搜索插入位置
35. 搜索插入位置
已解答
简单
相关标签
相关企业
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
题解
主要就是二分法,得好好练练,这道题实际上也是可以转换为二分的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
int l = 0, r = n - 1, ans = n;
while (l <= r) {
int mid = ((r - l) >> 1) + l;
if (target <= nums[mid]) {
ans = mid;
r = mid - 1;
}
else
l = mid + 1;
}
return ans;
}
|
74 搜索二维矩阵
74. 搜索二维矩阵
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
**输入:**matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
**输出:**true
**输入:**matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
**输出:**false
题解:
可以把二维矩阵展开成一维矩阵,只需要管理好映射关系即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if (matrix.size() == 0)
return false;
int m = matrix.size(), n = matrix[0].size();
int low = 0, high = m * n - 1;
while (low <= high) {
int mid = ((high - low) >> 1) + low;
int x = matrix[mid / n][mid % n];
if (x < target)
low = mid + 1;
else if (x > target)
high = mid - 1;
else
return true;
}
return false;
}
|
78 子集
78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
题解:
有点暴力哈,枚举,用每一位是否在当前的自己来枚举
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
vector<int> t;
vector<vector<int>> ans;
vector<vector<int>> subsets(vector<int>& nums) {
int n = nums.size();
for (int mask = 0; mask < (1 << n); ++mask) {
t.clear();
for (int i = 0; i < n; ++i) {
if (mask & (1 << i))
t.push_back(nums[i]);
}
ans.push_back(t);
}
return ans;
}
|
17 电话号码的字母组合
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
题解:
回溯相关的知识点还是太欠缺了啊,还得好好练练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
vector<string> letterCombinations(string digits) {
vector<string> combinations;
if (digits.empty())
return combinations;
unordered_map<char, string> phoneMap {
{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"}
};
string combination;
backtrack(combinations, phoneMap, digits, 0, combination);
return combinations;
}
void backtrack(vector<string> &combinations, unordered_map<char, string> &phoneMap, string &digits, int index, string &combination) {
if (index == digits.size())
combinations.push_back(combination);
else {
char digit = digits[index];
string &letters = phoneMap.at(digit);
for (const char &letter : letters) {
combination.push_back(letter);
backtrack(combinations, phoneMap, digits, index + 1, combination);
combination.pop_back();
}
}
}
|
39 组合总和
39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
题解:
依旧是回溯法,不过又来了个什么剪枝?得补习补习了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> ans;
vector<int> combine;
dfs(candidates, target, ans, combine, 0);
return ans;
}
void dfs(vector<int> &candidates, int target, vector<vector<int>> &ans, vector<int> &combine, int index) {
if (index == candidates.size())
return;
if (target == 0) {
ans.emplace_back(combine);
return;
}
dfs(candidates, target, ans, combine, index + 1);
if (target - candidates[index] >= 0) {
combine.emplace_back(candidates[index]);
dfs(candidates, target - candidates[index], ans, combine, index);
combine.pop_back();
}
}
|
22 括号生成
22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1
输出:["()"]
题解:
回溯真的是硬伤啊!!!😭
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
vector<string> generateParenthesis(int n) {
vector<string> result;
string current;
backtrack(result, current, 0, 0, n);
return result;
}
void backtrack(vector<string> &ans, string &cur, int open, int close, int n) {
if (cur.size() == n * 2) {
ans.push_back(cur);
return;
}
if (open < n) {
cur.push_back('(');
backtrack(ans, cur, open + 1, close, n);
cur.pop_back();
}
if (close < open) {
cur.push_back(')');
backtrack(ans, cur, open, close + 1, n);
cur.pop_back();
}
}
|
79 单词搜索
79. 单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出:true
示例 3:

输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出:false
题解:
用了牛客剑指Offer的一道类似的题的思路,做是做出来了,不过击败10%,太捞了,第一版一个普通递归回溯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
bool exist(vector<vector<char>>& board, string word) {
if (board.size() == 0)
return false;
int row = board.size();
int col = board[0].size();
vector<vector<bool>> flags(row, vector<bool>(col, false));
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if (exist(board, word, row, col, i, j, 0, flags))
return true;
}
}
return false;
}
bool exist(vector<vector<char>>& board, string word, int row, int col, int i, int j, int k, vector<vector<bool>> &flags) {
if (i < 0 || j < 0 || i >= row || j >= col || (board[i][j] != word[k]) || flags[i][j] == true)
return false;
if (k == word.size() - 1)
return true;
flags[i][j] = true;
if (exist(board, word, row, col, i + 1, j, k + 1, flags) ||
exist(board, word, row, col, i - 1, j, k + 1, flags) ||
exist(board, word, row, col, i, j + 1, k + 1, flags) ||
exist(board, word, row, col, i, j - 1, k + 1, flags))
return true;
flags[i][j] = false;
return false;
}
|
分割回文串
131. 分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是
回文串 。返回 s 所有可能的分割方案。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
题解:
差不多的,就是多了dfs的结合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
vector<vector<int>> flags;
vector<vector<string>> ret;
vector<string> ans;
int n;
public:
vector<vector<string>> partition(string s) {
n = s.size();
flags.assign(n, vector<int>(n, true));
for (int i = n - 1; i >= 0; --i) {
for (int j = i + 1; j < n; ++j) {
flags[i][j] = (s[i] == s[j]) && flags[i + 1][j - 1];
}
}
dfs(s, 0);
return ret;
}
void dfs(const string &s, int i) {
if (i == n) {
ret.push_back(ans);
return;
}
for (int j = i; j < n; ++j) {
if (flags[i][j]) {
ans.push_back(s.substr(i, j - i + 1));
dfs(s, j + 1);
ans.pop_back();
}
}
}
|
N皇后
51. N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
题解:
时隔这么久,我终于又有感觉了,一道困难题,也是对回溯法的一个锻炼提升
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
vector<vector<string>> solveNQueens(int n) {
vector<vector<string>> ans;
//标记列、斜对角是否有皇后
unordered_set<int> posCol = unordered_set<int>();
unordered_set<int> pos1 = unordered_set<int>();
unordered_set<int> pos2 = unordered_set<int>();
//用下标对应行,值对应列
vector<int> queens(n, -1);
//vector<string> ret;
backtrace(ans, posCol, pos1, pos2, queens, n, 0);
return ans;
}
void backtrace(vector<vector<string>> &ans, unordered_set<int> &posCol, unordered_set<int> &pos1, unordered_set<int> &pos2, vector<int> &queens, int n, int row) {
if (row == n) {
vector<string> board = generate(queens, n);
ans.push_back(board);
}
else {
for (int i = 0; i < n; ++i) {
if (posCol.find(i) != posCol.end())
continue;
int delta1 = row + i;
if (pos1.find(delta1) != pos1.end())
continue;
int delta2 = row - i;
if (pos2.find(delta2) != pos2.end())
continue;
queens[row] = i;
posCol.insert(i);
pos1.insert(delta1);
pos2.insert(delta2);
backtrace(ans, posCol, pos1, pos2, queens, n, row + 1);
queens[row] = -1;
posCol.erase(i);
pos1.erase(delta1);
pos2.erase(delta2);
}
}
}
vector<string> generate(vector<int> &queens, int n) {
vector<string> board = vector<string>();
for (int i = 0; i < n; ++i) {
string row(n, '.');
row[queens[i]] = 'Q';
board.push_back(row);
}
return board;
}
|
35 搜索插入位置
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
题解:
下面就开始二分咯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
int l = 0, r = n - 1, ans = n;
while (l <= r) {
int mid = ((r - l) >> 1) + l;
if (target <= nums[mid]) {
ans = mid;
r = mid - 1;
}
else
l = mid + 1;
}
return ans;
}
|
::感觉自己的思维真的不够打的开啊,局限性还存在
34 在排序数组中查找元素的第一个和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
题解:
二分法,巧妙利用一个flag区分了找左右边界的条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
vector<int> searchRange(vector<int>& nums, int target) {
int leftIndex = binarySearch(nums, target, true);
int rightIndex = binarySearch(nums, target, false) - 1;
if (leftIndex <= rightIndex && rightIndex < nums.size() && nums[leftIndex] == target && nums[rightIndex] == target)
return vector<int>{leftIndex, rightIndex};
return vector<int>{-1, -1};
}
int binarySearch(vector<int> &nums, int target, bool flag) {
int left = 0, right = nums.size() - 1, ans = nums.size();
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] > target || (flag && nums[mid] >= target)) {
right = mid - 1;
ans = mid;
}
else {
left = mid + 1;
}
}
return ans;
}
|
33 搜索旋转排序数组
33. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
题解:
二分查找,不过这里有很多细节,得注意下里面的判断条件:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
int search(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
if (nums.size() == 1) {
return nums[0] == target ? 0 : -1;
}
//二分查找
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target)
return mid;
if (nums[0] <= nums[mid]) {
if (nums[0] <= target && target < nums[mid])
right = mid - 1;
else
left = mid + 1;
}
else {
if (nums[mid] < target && target <= nums[nums.size() - 1]) //尤其是这里的条件,好好想想
left = mid + 1;
else
right = mid - 1;
}
}
return -1;
}
|
153 寻找旋转排序数组中的最小值
153. 寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4 次,则可以得到 [4,5,6,7,0,1,2]
- 若旋转
7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
题解:
二分查找一个小变化,理解本质了并不复杂:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int findMin(vector<int>& nums) {
if (nums.size() == 0) {
return -1;
}
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = l + ((r - l) >> 1);
if (nums[mid] > nums[r])
l = mid + 1;
else if (nums[mid] == nums[r])
--r;
else
r = mid;
}
return nums[l];
}
|
4 寻找两个正序数组的中位数
4. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
题解:
这题都能二分我是真没想到,主要关键点就是理解在两个数组上划分范围,以及各种特殊情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
if (nums1.size() > nums2.size())
return findMedianSortedArrays(nums2, nums1);
int m = nums1.size(), n = nums2.size();
int left = 0, right = m;
int preMin = 0, blackMax = 0;
while (left <= right) {
int mid1 = left + (right - left) / 2;
int mid2 = (m + n + 1) / 2 - mid1;
int mid1_left = (mid1 == 0 ? INT_MIN : nums1[mid1 - 1]);
int mid1_right = (mid1 == m ? INT_MAX : nums1[mid1]);
int mid2_left = (mid2 == 0 ? INT_MIN : nums2[mid2 - 1]);
int mid2_right = (mid2 == n ? INT_MAX : nums2[mid2]);
if (mid1_left <= mid2_right) {
preMin = max(mid1_left, mid2_left);
blackMax = min(mid1_right, mid2_right);
left = mid1 + 1;
}
else
right = mid1 - 1;
}
return (m + n) % 2 == 0 ? (preMin + blackMax) / 2.0 : preMin;
}
|
394
394. 字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
输入:s = "3[a]2[bc]"
输出:"aaabcbc"
示例 2:
输入:s = "3[a2[c]]"
输出:"accaccacc"
示例 3:
输入:s = "2[abc]3[cd]ef"
输出:"abcabccdcdcdef"
示例 4:
输入:s = "abc3[cd]xyz"
输出:"abccdcdcdxyz"
题解:
注意在栈中获取字符串时,不能简单粗暴的直接把字符拿到,因为每个字串中的字母顺序要保证好,直接拿的话后面在reverse的时候会被打乱
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
class Solution {
public:
string getDigits(string &s, int &index) {
string ret = "";
while (isdigit(s[index])) {
ret += s[index++];
}
return ret;
}
string conString(string s, int num) {
string ret = "";
while (num--) {
ret += s;
}
return ret;
}
string getString(vector<string> &str) {
string ret = "";
for (const string &s : str) {
ret += s;
}
return ret;
}
string decodeString(string s) {
vector<string> stk; //模拟栈
string ret = "";
int index = 0;
while (index < s.size()) {
char cur = s[index];
if (isdigit(cur)) {
string digits = getDigits(s, index);
stk.push_back(digits);
}
else if (isalpha(cur) || cur == '[') {
stk.push_back(string(1, s[index++]));
}
else {
++index;
vector<string> sub_str;
while (stk.back() != "[") {
sub_str.push_back(stk.back());
stk.pop_back();
}
reverse(sub_str.begin(), sub_str.end());
string t = getString(sub_str);
stk.pop_back();
int times = stoi(stk.back());
stk.pop_back();
string res;
res = conString(t, times);
stk.push_back(res);
}
}
for (const string &s : stk) {
ret += s;
}
return ret;
}
};
|
739 每日温度
739. 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
题解:
用单调栈,栈存放下标,只要下标在栈内说明该下标的温度还没有找到比它大的下一温度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size();
vector<int> ans(n, 0);
stack<int> stk;
if (n < 2) {
return ans;
}
for (int i = 0; i < n; ++i) {
while (!stk.empty() && temperatures[i] > temperatures[stk.top()]) {
int index = stk.top();
ans[index] = i - index;
stk.pop();
}
stk.push(i);
}
return ans;
}
|
198 打家劫舍
198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
题解:
动态规划,主要就是观察状态转换方程,找到了就很好求解了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
// 状态转换方程为 dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
// 注意边界条件即可
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.empty()) {
return 0;
}
int size = nums.size();
if (size == 1) {
return nums[0];
}
int first = nums[0], second = max(nums[1], nums[0]); // 边界条件
for (int i = 2; i < size; ++i) {
int temp = second;
second = max(first + nums[i], second);
first = temp;
}
return second;
}
};
|
279 完全平方数
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
题解:
动态规划版:找到其状态方程,主要就是理解F[n]等于啥
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int numSquares(int n) {
vector<int> f(n + 1, 0);
for (int i = 1; i <= n; ++i ) {
int minn = INT_MAX;
for (int j = 1; j * j <= i; ++j) {
minn = min(minn, f[i - j * j]);
}
f[i] = minn + 1;
}
return f[n];
}
};
|
数学版:多的不说,看官方题解就OK了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
bool isPerfectSquare(int n) {
int x = sqrt(n);
return x * x == n;
}
bool checkAnswer4(int n) {
while (n % 4 == 0) {
n /= 4;
}
return n % 8 == 7;
}
int numSquares(int n) {
if (isPerfectSquare(n)) {
return 1;
}
if (checkAnswer4(n)) {
return 4;
}
for (int i = 1; i * i <= n; ++i) {
int j = n - i * i;
if (isPerfectSquare(j)) {
return 2;
}
}
return 3;
}
};
|
322 零钱兑换
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
题解:
这道题和上面的完全平方数简直一模一样,只需要找到状态转移方程即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int maxNum = amount + 1;
vector<int> f(maxNum, maxNum);
f[0] = 0;
for (int i = 1; i <= amount; ++i) {
for (int j = 0; j < coins.size(); ++j) {
if (coins[j] <= i) {
f[i] = min(f[i], f[i - coins[j]] + 1);
}
}
}
return f[amount] > amount ? -1 : f[amount];
}
};
|
139 单词拆分
139. 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
**注意:**不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false
题解:
这道题其实也是动态规划的一种思路,只不过以前是数字,现在变成了字符串上的动态规划,需要提高一下思维能力啊,官方题解中还有剪枝的做法,可以考虑看看
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordDictSet = unordered_set<string>();
for (auto word : wordDict) {
wordDictSet.insert(word);
}
auto dp = vector<bool>(s.size() + 1);
dp[0] = true;
for (int i = 1; i <= s.size(); ++i) {
for (int j = 0; j < i; ++j) {
if (dp[j] && wordDictSet.find(s.substr(j, i - j)) != wordDictSet.end()) {
dp[i] = true;
break;
}
}
}
return dp[s.size()];
}
};
|
300 最长递增子序列
300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
题解:
第一版,暴力动态规划,找状态转移方程还是不熟练啊,没想到这还能直接找长度的方程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
if (n == 0) {
return 0;
}
vector<int> dp(n, 0);
for (int i = 0; i < n; ++i) {
dp[i] = 1;
for (int j = 0; j < i; ++j) {
if (nums[i] > nums[j]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
return *max_element(dp.begin(), dp.end());
}
};
|
第二版,动态规划+贪心,真贪
152 乘积最大子数组
152. 乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组
(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32位 整数。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
题解:
很优雅的动态规划,我一开始只解决了一半,没有考虑到负负得正的情况,其实有两个状态转移方程,一个保存最大,一个保存最小,然后优化一下,用整形变量模拟dp数组(这道题最迷惑的事整型溢出问题,非要加这个干么,还得用别的类型解决)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
int maxProduct(vector<int>& nums) {
int n = nums.size();
if (n == 0) {
return 0;
}
double maxDp = nums[0], minDp = nums[0], ans = nums[0]; // 用double防整型溢出
for (int i = 1; i < n; ++i) {
double mx = maxDp, mi = minDp;
maxDp = max(mx * nums[i], max(mi * nums[i], static_cast<double>(nums[i])));
minDp = min(mx * nums[i], min(mi * nums[i], static_cast<double>(nums[i])));
ans = max(ans, maxDp);
}
return static_cast<int>(ans);
}
};
|
416 分割等和子集
416. 分割等和子集 - 力扣(LeetCode)
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
题解:
第一次自己做想到简单的单个累加,只要大于总和的一半就舍弃,其实这样做可能漏掉选项。。。只能说还是考虑的不够充分,这道题需要动态规划,没有那么简单
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n = nums.size();
if (n < 2) {
return false;
}
int sum = 0, maxNum = 0;
for (int a : nums) {
sum += a;
maxNum = max(maxNum, a);
}
// 和为奇数,不可能分割
if (sum % 2 != 0) {
return false;
}
int target = sum >> 1;
if (maxNum > target) {
return false;
}
/*
dp[i][j]表示能否在[0, i]范围选取一些数使其和为j
边界条件:
1. j = 0: 选0个数即可,所以dp[i][0]永为true
2. i = 0: 只能选0或者nums[0]这个数,所以dp[0][0]、dp[0][nums[0]]为true
其余情况:
1. j >= nums[i]:即nums[i]加进来后的和可能大于、小于、等于j,要么加要么不加
只需要将加和不加的情况或运算保存即可;
如果加进来,需要保证和等于j所以此时的和
一定为j - nums[i],需要寻找和为j - nums[i]的那一列,又因为加进来的数的下标为i,所以
需要寻找下标为i - 1的那一行,总结需要判断dp[i - 1][j - nums[i]]的真假
如果不加进来,一样的思路可以知道需要判断dp[i - 1][j]的真假,最后可以得出状态转移
方程:dp[i][j] = dp[i - 1][j - nums[i]] | dp[i - 1][j];
2. j < nums[i]:nums[i]不可能加进来,所以dp[i][j] = dp[i - 1][j]
*/
vector<vector<int>> dp(n, vector<int>(target + 1, 0));
for (int i = 0; i < n; ++i) {
dp[i][0] = true;
}
dp[0][nums[0]] = true;
for (int i = 1; i < n; ++i) {
int num = nums[i];
for (int j = 1; j <= target; ++j) {
if (j >= num) {
dp[i][j] = dp[i - 1][j] | dp[i - 1][j - nums[i]];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n - 1][target];
}
};
|
上面的代码用到了二维数组辅助记录状态,可以更加优化,注意到了每一次dp只与上一行有关,所以可以使用一维数组代替:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n = nums.size();
if (n < 2) {
return false;
}
int sum = 0, maxNum = 0;
for (int a : nums) {
sum += a;
maxNum = max(maxNum, a);
}
// 和为奇数,不可能分割
if (sum % 2 != 0) {
return false;
}
int target = sum >> 1;
if (maxNum > target) {
return false;
}
/*
i 表示目前遍历数组元素的下标
dp[j]表示能否在[0, i]范围选取一些数使其和为j
边界条件:
1. j = 0: 选0个数即可,所以dp[0]为true
其余情况:
1. j >= nums[i]:即nums[i]加进来后的和可能大于、小于、等于j,要么加要么不加
只需要将加和不加的情况或运算保存即可;
简化一下上一个版本代码可以得到:dp[j] |= dp[j - nums[i]];
2. j < nums[i]:nums[i]不可能加进来,不对dp[j]做修改
注意:
更新一维数组只能从高向低更新,因为高位会用到低位的状态。
*/
vector<int> dp(target + 1, 0);
dp[0] = true;
for (int i = 1; i < n; ++i) {
int num = nums[i];
// 根据上面二维数组的代码可以知道,只有>=num的时候才做运算,其他不做操作
// 所以此处的for循环写成这样
for (int j = target; j >= num; --j) {
dp[j] |= dp[j - nums[j]];
}
}
return dp[target];
}
};
|
::这道题也是卡了老久了,从6月份开始,咱也不知道当时咋回事,脑子好像就是转不动了,最近调理身体,早睡早起,感觉精神好多了,一下就理解了这道题的含义。
32 最长有效括号
32. 最长有效括号
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
示例 3:
输入:s = ""
输出:0
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
class Solution {
public:
/*
动态规划
首先考虑到格式正确的括号一定是这样的形式:"()"可以
知道一定是以")"结束,所以只需要寻找")"出现的位置即可
用dp[i]表示在字符串s的i位置最长括号字串有多长,则
1. s[i] == ")" && s[i - 1] == "("
此时dp[i] = dp[i - 2] + 2;
2. s[i] == ")" && s[i - 1] == ")"
此时需要考虑是否存在(())的情况,先说公式
dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2;
解释:dp[i - 1]是因为前一个字符是")"所以要加上其dp值,后面部分
dp[i - dp[i - 1] - 2]是在定位到最近的没有算进本次dp中的位置,防止漏加
最后的2是一对括号
最后需要注意中括号内的不能越界
*/
int longestValidParentheses(string s) {
int n = s.size();
int maxans = 0;
if (n < 2) {
return 0;
}
vector<int> dp(n , 0);
for (int i = 1; i < n; ++i) {
if (s[i] == ')') {
if (s[i - 1] == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s[i - dp[i - 1] - 1] == '('){ //这里的条件也十分重要
dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxans = max(maxans, dp[i]);
}
}
return maxans;
}
};
|
这道题还有一个常常数级变量的办法,之后再考虑
62 不同路径
::自己做出来的,不错,刷了这么多题还是有点效果了
62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
/*
动态规划
准备一个二维数组dp用于分析中间状态,dp[i][j]表示(i, j)位置有几种到法,
当前格子的dp应当等于其左侧和上侧格子的dp值(存在的话)。
考虑以下情况:
1. 起点下侧和右侧若有格子,则其dp为1
2. dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
*/
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 0));
if (m < 1 || n < 1) return 0;
// 起点
dp[0][0] = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 && j == 0) continue; // 之前用的break,就是不对
dp[i][j] = ((i - 1) >= 0 ? dp[i - 1][j] : 0) + ((j - 1) >= 0 ? dp[i][j - 1] : 0);
}
}
return dp[m - 1][n - 1];
}
};
|
理论上应该还可以优化空间,今天就先到这里
64 最小路径和
64. 最小路径和
给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
**说明:**每次只能向下或者向右移动一步。
示例 1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
题解:
思路和上一道题一模一样:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
/*
dp[i][j]表示[i, j]格子上的最小和,最终结果为dp[m - 1][n - 1]
注意边界问题即可
dp[i][j] = min(((i - 1) > 0 ? dp[i - 1][j] : 0), ((j - 1) > 0 ? dp[i][j - 1] : 0)) + grid[i][j]
*/
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
if (m < 1 && n < 1) {
return 0;
}
vector<vector<int>> dp(m, vector<int>(n, 0));
dp[0][0] = grid[0][0];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 && j == 0) continue;
// 注意细节,这里应该是>=0,之前填了个>0不正确
int leftdp = ((i - 1) >= 0 ? dp[i - 1][j] : INT_MAX);
int topdp = ((j - 1) >= 0 ? dp[i][j - 1] : INT_MAX);
dp[i][j] = min(leftdp, topdp) + grid[i][j];
}
}
return dp[m - 1][n - 1];
}
};
|
不过这样子做肯定不是最优的,还有更优秀的解法,后面再优化。
5 最长回文字串
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的 回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
题解:
已经是第二次做这个题了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
public:
/*
方法大概意思就是一直找回文串。。不断更新
长度
*/
string longestPalindrome(string s) {
int n = s.size();
if (n < 1) {
return "";
}
int start = 0, end = 0;
for (int i = 0; i < n; ++i) {
auto [left1, right1] = help(s, i, i);
auto [left2, right2] = help(s, i, i + 1);
if (right1 - left1 > end - start) {
end = right1;
start = left1;
}
if (right2 - left2 > end - start) {
end = right2;
start = left2;
}
}
return s.substr(start, end - start + 1);
}
/*
具体找回文串的函数,思路也很简单
*/
pair<int, int> help(string &s, int i, int j) {
while (i >= 0 && j < s.size() && s[i] == s[j]) {
--i;
++j;
}
// 注意此时的i,j对应着不符合回文条件的,所以要回退一个状态
return {i + 1, j - 1};
}
};
|
1143 最长公共子序列
1143. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。
题解:
虽然这道题没有自己想出来,但是起码还是反应比以前快了,可以做出来了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public:
/*
动态规划:
dp[i][j] 表示在text1上长度为i,text2上长度为j的最长公共子序列
考虑边界条件:
1. 当i = 0或j = 0时,绝对不可能有公共序列,所以i = 0或j = 0时dp为0
2. 当i和j都大于0时:
- text1[i - 1] = text2[j - 1]时,说明正好时一对公共字符,此时的
dp只需要加上这一对公共字符即可,所以dp[i][j] = dp[i - 1][j - 1] + 1
- text1[i - 1] != text2[j - 1]时,说明这一对不是公共字符,两边分别往前面看
一个字符,看看前面的那个字符是否可以凑个最长:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
这里无需再考虑越界问题,因为=0的情况在上面
*/
int longestCommonSubsequence(string text1, string text2) {
int n1 = text1.length(), n2 = text2.length();
if (n1 < 1 || n2 < 1) return 0;
vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1, 0));
// 不用考虑0,直接从1开始,上限应是<=
for (int i = 1; i <= n1; ++i) {
char c1 = text1.at(i - 1);
for (int j = 1; j <= n2; ++j) {
char c2 = text2.at(j - 1);
if (c1 == c2) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[n1][n2];
}
};
|
72 编辑距离
72. 编辑距离
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
题解:
这道题也直接记住吧,动态规划难点就在于找到状态转移方程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
class Solution {
public:
/*
PS:这是难题啊,写个中等难度骗狗呢
动态规划:
dp[i][j]表示word1前i个字母和word2前j个字母
转换得最小步骤数。
可以知道word1中删除字符等同于在word2中插入字符
word2中删除字符等同于在word1中插入字符于是我们
可以得到操作不同的情况:
1. A中插入字符(比如ba和ab的情况,必须插入一个步骤才更少)
此时dp[i][j] = dp[i][j - 1] + 1
2. B中插入字符
此时dp[i][j] = dp[i - 1][j] + 1
3. A中替f换字符
- 若word1[i] != word2[j]
此时dp[i][j] = dp[i - 1][j - 1] + 1(多一步替换)
- 否则
dp[i][j] = dp[i - 1][j - 1]
以上三种情况取最小步骤即可
考虑边界条件:
i = 0时,需要j步达到相同,反之亦然
*/
int minDistance(string word1, string word2) {
int m = word1.size(), n = word2.size();
if (n * m == 0) return n + m; // 有一个空串
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
// 处理边界条件
for (int i = 0; i <= m; ++i) {
dp[i][0] = i;
}
for (int j = 0; j <= n; ++j) {
dp[0][j] = j;
}
// 动态规划
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
int left = dp[i - 1][j] + 1;
int down = dp[i][j - 1] + 1;
int left_down = dp[i - 1][j - 1];
if (word1[i - 1] != word2[j - 1]) left_down += 1;
dp[i][j] = min(left, min(down, left_down));
}
}
return dp[m][n];
}
};
|
31 下一个排列
31. 下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,
arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,
arr = [1,2,3] 的下一个排列是 [1,3,2] 。
- 类似地,
arr = [2,3,1] 的下一个排列是 [3,1,2] 。
- 而
arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须** 原地 **修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
题解:
我们希望下一个数 比当前数大,这样才满足 “下一个排列” 的定义。因此只需要 将后面的「大数」与前面的「小数」交换,就能得到一个更大的数。比如 123456,将 5 和 6 交换就能得到一个更大的数 123465。
我们还希望下一个数 增加的幅度尽可能的小,这样才满足“下一个排列与当前排列紧邻“的要求。为了满足这个要求,我们需要:
在 尽可能靠右的低位 进行交换,需要 从后向前 查找
将一个 尽可能小的「大数」 与前面的「小数」交换。比如 123465,下一个排列应该把 5 和 4 交换而不是把 6 和 4 交换
将「大数」换到前面后,需要将「大数」后面的所有数 重置为升序,升序排列就是最小的排列。以 123465 为例:首先按照上一步,交换 5 和 4,得到 123564;然后需要将 5 之后的数重置为升序,得到 123546。显然 123546 比 123564 更小,123546 就是 123465 的下一个排列
以上就是求 “下一个排列” 的分析过程。
算法过程
标准的 “下一个排列” 算法可以描述为:
从后向前 查找第一个 相邻升序 的元素对 (i,j),满足 A[i] < A[j]。此时 [j,end) 必然是降序
在 [j,end) 从后向前 查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
将 A[i] 与 A[k] 交换
可以断定这时 [j,end) 必然是降序,逆置 [j,end),使其升序
如果在步骤 1 找不到符合的相邻元素对,说明当前 [begin,end) 为一个降序顺序,则直接跳到步骤 4
该方法支持数据重复,且在 C++ STL 中被采用。
非常巧妙的思路啊,不过幸好看了题解自己还是能理解并写出相应的代码解决问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
void nextPermutation(vector<int>& nums) {
if (nums.size() == 0) {
return;
}
int i = nums.size() - 2;
int j = nums.size() - 1;
int k = nums.size() - 1;
while (i >= 0 && nums[i] >= nums[j]) {
--i;
--j;
}
if (i >= 0) {
while (k > 0 && nums[i] >= nums[k]) {
--k;
}
swap(nums[i], nums[k]);
}
i = j;
j = nums.size() - 1;
while (i < j) {
swap(nums[i], nums[j]);
++i, --j;
}
}
};
|
287 寻找重复数
287. 寻找重复数
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
示例 3 :
输入:nums = [3,3,3,3,3]
输出:3
题解:
非常厉害的二分法,绝了:
我们定义 cnt[i] 表示 nums 数组中小于等于 i 的数有多少个,假设我们重复的数是 target,那么 [1,target−1]里的所有数满足 cnt[i]≤i,[target,n] 里的所有数满足 cnt[i]>i,具有单调性。
以示例 1 为例,我们列出每个数字的 cnt 值:
nums 1 2 3 4
cnt 1 3 4 5
示例中重复的整数是 2,我们可以看到 [1,1] 中的数满足 cnt[i]≤i,[2,4] 中的数满足 cnt[i]>i 。
如果知道 cnt[] 数组随数字 i 逐渐增大具有单调性(即 target 前 cnt[i]≤i,target 后 cnt[i]>i),那么我们就可以直接利用二分查找来找到重复的数。
但这个性质一定是正确的吗?考虑 nums 数组一共有 n+1 个位置,我们填入的数字都在 [1,n] 间,有且只有一个数重复放了两次以上。对于所有测试用例,考虑以下两种情况:
如果测试用例的数组中 target 出现了两次,其余的数各出现了一次,这个时候肯定满足上文提及的性质,因为小于 target 的数 i 满足 cnt[i]=i,大于等于 target 的数 j 满足 cnt[j]=j+1。
如果测试用例的数组中 target 出现了三次及以上,那么必然有一些数不在 nums 数组中了,这个时候相当于我们用 target 去替换了这些数,我们考虑替换的时候对 cnt[] 数组的影响。如果替换的数 i 小于 target ,那么 [i,target−1] 的 cnt 值均减一,其他不变,满足条件。如果替换的数 j 大于等于 target,那么 [target,j−1] 的 cnt 值均加一,其他不变,亦满足条件。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int n = nums.size();
int l = 0, r = n - 1, ans = -1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
int cnt = 0;
for (int i = 0; i < n; ++i) {
cnt += (nums[i] <= mid); // 循环寻找cnt
}
if (cnt <= mid) {
l = mid + 1;
}
else {
r = mid - 1;
ans = mid;
}
}
return ans;
}
};
|
面试经典150
88 合并两个有序数组
88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
**注意:**最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
题解:
coding问题,半年前做的题了,久远啊
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
/*
双指针
虽然是一道简单题,但是想要做到最优解可不简单:
我们可以从后往前插入元素,因为nums1的尾部一定是空的,每次从选取较大的
插入nums1尾部,从nums1[m - 1]和nums2[n - 1]开始遍历,一定不会越界,
因为题目告诉我们nums1长度为m + n.
*/
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int p1 = m - 1, p2 = n - 1;
int tail = m + n - 1;
int cur = 0;
// 这里要用或,因为是要将两个数组都遍历完
while (p1 >= 0 || p2 >= 0) {
// nums1越界了, 直接将nums2目前的值保存下来后面填入
if (p1 == -1) {
cur = nums2[p2--];
} else if (p2 == -1) {
cur = nums1[p1--];
} else if (nums1[p1] > nums2[p2]) {
cur = nums1[p1--];
} else {
cur = nums2[p2--];
}
nums1[tail--] = cur;
}
return;
}
};
|
27 移除元素
27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
- 更改
nums 数组,使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
- 返回
k。
用户评测:
评测机将使用以下代码测试您的解决方案:
int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
// 它以不等于 val 的值排序。
int k = removeElement(nums, val); // 调用你的实现
assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
assert nums[i] == expectedNums[i];
}
如果所有的断言都通过,你的解决方案将会 通过。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2,_,_]
解释:你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3,_,_,_]
解释:你的函数应该返回 k = 5,并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
题解:
数组问题双指针真是妙用啊
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public:
/*
双指针
题目讲的花里胡哨,其实只需要将nums中为val的元素移到末尾即可,
使用双指针实现,left从0开始,right从nums.size()开始,如果
nums[left] == val,则将nums[left]的值改为nums[right - 1]
知道left和right相遇。
至于为什么right是从nums.size()开始?是为了方便最后left == right的
时候直接返回left,就不用+1了。
*/
int removeElement(vector<int>& nums, int val) {
int n = nums.size();
if (n < 1) {
return 0;
}
int left = 0, right = n;
while (left < right) {
if (nums[left] == val) {
nums[left] = nums[right - 1];
--right;
} else {
left++;
}
}
return left;
}
};
|
26 删除有序数组中的重复项
26. 删除有序数组中的重复项
给你一个 非严格递增排列 的数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
- 返回
k 。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
题解:
::一开始看错题了,服了,以为数组是乱序的,搞半天
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
/*
双指针:
这道题一开始没有搞懂,还以为是乱序的,结果仔细一看是排好序的
这就简单了:
准备两个指针,i代表替换元素的位置,j代表遍历的位置
从数组的1位置开始即可,++j,只要发现nums[j - 1] != nums[j]
则将此时的nums[j]填入i位置,并++i
*/
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
if (n < 2) {
return n;
}
int i = 1, j = 1;
while (j < n) {
if (nums[j] != nums[j - 1]) {
nums[i] = nums[j];
++i;
}
++j;
}
return i;
}
};
|
80 删除有序数组中的重复项II
80. 删除有序数组中的重复项 II
给你一个有序数组 nums ,请你** 原地** 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以**「引用」**方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝
int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [1,1,1,2,2,3]
输出:5, nums = [1,1,2,2,3]
解释:函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。 不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,1,2,3,3]
输出:7, nums = [0,0,1,1,2,3,3]
解释:函数应返回新长度 length = 7, 并且原数组的前七个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。
题解:
自己做的,时间不错,空间也还行
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution {
public:
/*
双指针:
- 准备一对快慢指针,快指针遍历数组,满指针用于存放元素
- 准备一个变量count,表示nums[fast]出现的次数
- 遍历数组(++fast)使nums[fast] != nums[fast - 1]
- 如果count > 2令其等于2
- 循环count次,每次执行nums[slow++] = nums[fast - 1]
- 返回slow
考虑边界条件:
- nums长度小于等于2,直接返回长度不做修改即可
- nums长度大于2,最后nums[0]一定不会被修改,但是由于count
统计次数,所以从0开始遍历
- fast遍历到最后一定会越界,所以越界条件应该是fast > n
*/
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
if (n <= 2) return n;
int fast = 0, slow = 0;
int count = 0;
while (fast <= n) {
// 这里的fast==n一定要写前面,防止后面条件越界
if (fast == n || (fast > 0 && nums[fast - 1] != nums[fast])) {
count = count > 2 ? 2 : count;
int temp = nums[fast - 1];
while (count) {
nums[slow] = temp;
++slow;
--count;
}
}
++count;
++fast;
}
return slow;
}
};
|
169 多数元素
169. 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
题解:
这道题基础做法可以用哈希表辅助,不过当然,我是不会只追求基础的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public:
/*
Boyer-Moore投票算法:
- 准备两个变量cur和count分别表示一个候选众数和他出现的次数
- 初始时count = 0,直接将nums[0]赋予cur,++count
- 遍历数组,知道遇到不等于cur的--count
- 若count再次为0则将此时的元素赋予cur,++count
- 重复上述流程直至遍历完成,最后的cur一定是要找的众数
*/
int majorityElement(vector<int>& nums) {
int cur = -1, count = 0;
for (int i = 0; i < nums.size(); ++i) {
if (count == 0) {
cur = nums[i];
++count;
} else if (cur == nums[i]) {
++count;
} else {
--count;
}
}
return cur;
}
};
|
189 轮转数组
189. 轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
/*
翻转数组:
- 看了题解,不禁感叹妙啊
- 翻转整个数组
- 翻转[0, k mod n - 1]范围上的子数组
- 翻转[k mod n, n - 1]范围上的子数组
优雅,太优雅了.模运算真的是个神奇的东西
*/
void reverse(vector<int> &nums, int start, int end) {
while (start < end) {
swap(nums[start], nums[end]);
++start;
--end;
}
}
void rotate(vector<int>& nums, int k) {
int n = nums.size();
if (n < 2) return;
k %= n;
reverse(nums, 0, n - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, n - 1);
}
};
|
121 买卖股票的最佳时机
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
/*
一次遍历:
只需要维护好最小买入价格和最大利润
- 两个变量分别表示最小买入价和最大利润
- 遍历数组,维护买入价和最大利润
由于当前遍历到元素的一定不会在上一个维护的最小买入价
之前,所以一定正确。
*/
int maxProfit(vector<int>& prices) {
int n = prices.size();
if (n < 2) return 0;
int minPrice = INT_MAX, maxProfit = 0;
for (const int a : prices) {
minPrice = min(minPrice, a);
maxProfit = max(maxProfit, a - minPrice);
}
return maxProfit;
}
};
|
买卖股票的最佳时机II
122. 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0。
题解:
妙啊妙啊
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
/*
和买卖股票的最佳时机不同在于这道题可以
买卖两支甚至三支股票,只不过同一时间最多
只有一支
贪心算法:
根据题目意思,结果应是某n个区间上的两头元素差之和
例如prices[i] - prices[j],该式子可以分解为
prices[i] - prices[i - 1] + prices[i - 1] - prices[i - 2] ... - prices[j]
可以看出其实就是长度为1区间累加和的值,只需要让小于0的以0累加即可
求得最大值
*/
int maxProfit(vector<int>& prices) {
int n = prices.size();
if (n < 2) return 0;
int ans = 0;
for (int i = 1; i < n; ++i) {
ans += max(0, (prices[i] - prices[i - 1]));
}
return ans;
}
};
|
55 跳跃游戏
55. 跳跃游戏
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
/*
贪心:
1. 遍历数组
2. 维护一个maxpos表示能到达的最大位置
3. 如果maxpos >= n - 1则可以到达反之不可
*/
bool canJump(vector<int>& nums) {
int n = nums.size();
if ( n < 1) return false;
int maxpos = 0;
for (int i = 0; i < n; ++i) {
if (i <= maxpos) {
maxpos = max(maxpos, i + nums[i]);
if (maxpos >= n - 1) {
return true;
}
}
}
return false;
}
};
|
45 跳跃游戏II
45. 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
/*
思路与上题差不多
*/
int jump(vector<int>& nums) {
int n = nums.size();
if (n <= 1) return 0;
int step = 0;
int maxpos = 0;
int end = 0;
// 注意条件,最后的目的地n - 1不应该遍历到
for (int i = 0; i < n - 1; ++i) {
if (i <= maxpos) {
maxpos = max(maxpos, i + nums[i]);
if (i == end) {
end = maxpos;
++step;
}
}
}
return step;
}
};
|
274 H指数
274. H 指数
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。
根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发表了 h 篇论文,并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值,h 指数 是其中最大的那个。
示例 1:
输入:citations = [3,0,6,1,5]
输出:3
解释:给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3。
示例 2:
输入:citations = [1,3,1]
输出:1
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
class Solution {
public:
/*
翻译题目的意思就是找到数组中的某个数x,使得
数组中刚好有x个数满足大于等于x,并且x要尽可能大
二分法:
虽然数组是无序的,但是数组下标是有序的
我们对数组下标二分,直到找到符合题意的mid
考虑边界情况:
数组只有一个数且为0,此时left和right不会更新,
所以mid的条件需要考虑。可以在分母上多加1来避免
*/
int hIndex(vector<int>& citations) {
int left = 0, right = citations.size();
int mid = 0, cnt = 0;
while (left < right) {
mid = left + ((right - left + 1) >> 1);
cnt = 0;
for (const int a : citations) {
if (a >= mid) {
++cnt;
}
}
if (cnt >= mid) {
left = mid;
} else {
right = mid - 1;
}
}
return left;
}
};
|
380 O(1)时间插入、删除和获取随机元素
380. O(1) 时间插入、删除和获取随机元素
实现RandomizedSet 类:
RandomizedSet() 初始化 RandomizedSet 对象bool insert(int val) 当元素 val 不存在时,向集合中插入该项,并返回 true ;否则,返回 false 。bool remove(int val) 当元素 val 存在时,从集合中移除该项,并返回 true ;否则,返回 false 。int getRandom() 随机返回现有集合中的一项(测试用例保证调用此方法时集合中至少存在一个元素)。每个元素应该有 相同的概率 被返回。
你必须实现类的所有函数,并满足每个函数的 平均 时间复杂度为 O(1) 。
示例:
输入
["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"]
[[], [1], [2], [2], [], [1], [2], []]
输出
[null, true, false, true, 2, true, false, 2]
解释
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // 向集合中插入 1 。返回 true 表示 1 被成功地插入。
randomizedSet.remove(2); // 返回 false ,表示集合中不存在 2 。
randomizedSet.insert(2); // 向集合中插入 2 。返回 true 。集合现在包含 [1,2] 。
randomizedSet.getRandom(); // getRandom 应随机返回 1 或 2 。
randomizedSet.remove(1); // 从集合中移除 1 ,返回 true 。集合现在包含 [2] 。
randomizedSet.insert(2); // 2 已在集合中,所以返回 false 。
randomizedSet.getRandom(); // 由于 2 是集合中唯一的数字,getRandom 总是返回 2 。
题解:
这道题纯Coding问题,跟算法关系不大
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
class RandomizedSet {
public:
/*
使用数组+哈希表实现,哈希表用于O(1)的时间查找
数组用于O(1)的时间随机访问元素。
插入:
1. 判断val是否在哈希表中,在则不做操作
2. 不在则将val添加到数组末尾并更新哈希表
删除:
1. 判断val是否在哈希表中,不在则不做操作
2. 在则将数组末尾元素移动至val对应的位置
3. 更新维护哈希表
3. 删除数组末尾元素,并删除哈希表中对应元素
获取随机值:
- 获取一个随机下标返回元素
*/
RandomizedSet() {
srand((unsigned)time(NULL));
}
bool insert(int val) {
if (indices.count(val)) {
return false;
}
int index = nums.size();
nums.emplace_back(val);
indices[val] = index;
return true;
}
bool remove(int val) {
if (!indices.count(val)) {
return false;
}
int index = indices[val];
int last = nums.back();
nums[index] = last;
indices[last] = index;
nums.pop_back();
indices.erase(val);
return true;
}
int getRandom() {
int index = rand() % nums.size();
return nums[index];
}
private:
vector<int> nums;
unordered_map<int, int> indices;
};
/**
* Your RandomizedSet object will be instantiated and called as such:
* RandomizedSet* obj = new RandomizedSet();
* bool param_1 = obj->insert(val);
* bool param_2 = obj->remove(val);
* int param_3 = obj->getRandom();
*/
|
238 除自身以外数组的乘积
238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 **不要使用除法,**且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
/*
两次遍历
1. 从1到n - 1遍历数组,每次用ans[i - 1] * nums[i - 1]更新ans[i]
2. 从n - 2到0遍历数组,用一个temp变量保存累乘值,并更新到相应的
ans中
*/
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
if (n == 0) return {};
vector<int> ans(nums.size(), 1);
int temp = 1;
for (int i = 1; i < n; ++i) {
ans[i] *= ans[i - 1] * nums[i - 1];
}
for (int i = n - 2; i >= 0; --i) {
temp *= nums[i + 1];
ans[i] *= temp;
}
return ans;
}
};
|
代码随想录
数组
704 二分查找
704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public:
/*
二分查找,道理是明白了,就是写代码莫名其妙的
1. 找到左右边界
2. 找到中间点,开始二分
3. 如果中间值小于目标则左边界右移,反之右边界左移
4. 知道找到位置或者最后退出
ps: 为什么会一看就会一写就废,其实是因为对区间的定义没有理解:
- 这里代码的区间为[l, r],左闭右闭,所以在while里面应当写l <= r,
因为l = r的时候在[l, r]区间内是有意义的,并且因为该区间右闭,所以
当nums[mid] > target时r = mid - 1,因为区间的定义使得r应当是可取的;
- 如果一开始r的定义为r = n,则此时while里的条件应该改成l < r,因为
l = r在[l, r)区间内无意义,l 不可能等于r。此时当nums[mid] > target时
r = mid,因为区间的定义,r应当不可取
*/
int search(vector<int>& nums, int target) {
int n = nums.size();
if (n == 0) return -1;
int l = 0, r = n - 1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
int num = nums[mid];
if (num == target) {
return mid;
} else if (num < target) {
l = mid + 1;
} else {
r = mid - 1;
}
}
return -1;
}
};
|
27 移除元素
27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
- 更改
nums 数组,使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
- 返回
k。
用户评测:
评测机将使用以下代码测试您的解决方案:
int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
// 它以不等于 val 的值排序。
int k = removeElement(nums, val); // 调用你的实现
assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
assert nums[i] == expectedNums[i];
}
如果所有的断言都通过,你的解决方案将会 通过。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2,_,_]
解释:你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3,_,_,_]
解释:你的函数应该返回 k = 5,并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public:
/*
双指针
题目讲的花里胡哨,其实只需要将nums中为val的元素移到末尾即可,
使用双指针实现,left从0开始,right从nums.size()开始,如果
nums[left] == val,则将nums[left]的值修改为nums[right - 1]的值,
直到left和right相遇。
至于为什么right是从nums.size()开始?是为了方便最后left == right的
时候直接返回left,就不用+1了。
*/
int removeElement(vector<int>& nums, int val) {
int n = nums.size();
if (n < 1) {
return 0;
}
int left = 0, right = n;
while (left < right) {
if (nums[left] == val) {
nums[left] = nums[right - 1];
--right;
} else {
left++;
}
}
return left;
}
};
|
977 有序数的平方
977. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
题解:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
class Solution {
public:
/*
有简单的暴力方法:
1. 首先遍历数组,更新数组每个元素等于其自身平方;
2. 对处理后的数组排序;
3. 返回排序后的数组。
这个方法的时间复杂度为O(n + nlogn),相当差,但是简单
更好的方法双指针:
注意到数组的元素有正负,而负数的平方可能最后比本来数组
里正数的平方更大,所以了解到新数组的最大值可能在原数组
左右两边处理得到,不会在中间,所以可以借用归并排序的思
想:
1. 准备两个指针,left和right,另准备一个和原数组一样
大的新数组用于存放结果
2. 准备一个指针,point,用来表示目前插入新数组的位置
并比较left和right对应元素的平方的大小,将大的放入point
位置,循环此步骤直到left和right相遇
3. 返回新数组
*/
vector<int> sortedSquares(vector<int>& nums) {
int n = nums.size();
if (n == 0) return {};
int left = 0, right = n - 1;
vector<int> ans(n, 0);
int p = n - 1;
while (left <= right) {
int l = nums[left] * nums[left];
int r = nums[right] * nums[right];
if (l > r) {
++left;
ans[p--] = l;
} else {
--right;
ans[p--] = r;
}
}
return ans;
}
};
|
高频SQL50题
1757 可回收且低脂的产品
1757. 可回收且低脂的产品
表:Products
+-------------+---------+
| Column Name | Type |
+-------------+---------+
| product_id | int |
| low_fats | enum |
| recyclable | enum |
+-------------+---------+
product_id 是该表的主键(具有唯一值的列)。
low_fats 是枚举类型,取值为以下两种 ('Y', 'N'),其中 'Y' 表示该产品是低脂产品,'N' 表示不是低脂产品。
recyclable 是枚举类型,取值为以下两种 ('Y', 'N'),其中 'Y' 表示该产品可回收,而 'N' 表示不可回收。
编写解决方案找出既是低脂又是可回收的产品编号。
返回结果 无顺序要求 。
返回结果格式如下例所示:
示例 1:
输入:
Products 表:
+-------------+----------+------------+
| product_id | low_fats | recyclable |
+-------------+----------+------------+
| 0 | Y | N |
| 1 | Y | Y |
| 2 | N | Y |
| 3 | Y | Y |
| 4 | N | N |
+-------------+----------+------------+
输出:
+-------------+
| product_id |
+-------------+
| 1 |
| 3 |
+-------------+
解释:
只有产品 id 为 1 和 3 的产品,既是低脂又是可回收的产品。
题解:
1
2
3
4
|
# 基础SQL
# Write your MySQL query statement below
select product_id from Products
where low_fats = "Y" and recyclable = "y";
|
584 寻找用户推荐人
584. 寻找用户推荐人
表: Customer
+-------------+---------+
| Column Name | Type |
+-------------+---------+
| id | int |
| name | varchar |
| referee_id | int |
+-------------+---------+
在 SQL 中,id 是该表的主键列。
该表的每一行表示一个客户的 id、姓名以及推荐他们的客户的 id。
找出那些 没有被 id = 2 的客户 推荐 的客户的姓名。
以 任意顺序 返回结果表。
结果格式如下所示。
示例 1:
输入:
Customer 表:
+----+------+------------+
| id | name | referee_id |
+----+------+------------+
| 1 | Will | null |
| 2 | Jane | null |
| 3 | Alex | 2 |
| 4 | Bill | null |
| 5 | Zack | 1 |
| 6 | Mark | 2 |
+----+------+------------+
输出:
+------+
| name |
+------+
| Will |
| Jane |
| Bill |
| Zack |
+------+
题解:
1
2
3
4
|
# 需要注意该列具可为null,需要判断
# Write your MySQL query statement below
select name from Customer
where referee_id <> 2 or referee_id is null;
|
595 大的国家
595. 大的国家
World 表:
+-------------+---------+
| Column Name | Type |
+-------------+---------+
| name | varchar |
| continent | varchar |
| area | int |
| population | int |
| gdp | bigint |
+-------------+---------+
name 是该表的主键(具有唯一值的列)。
这张表的每一行提供:国家名称、所属大陆、面积、人口和 GDP 值。
如果一个国家满足下述两个条件之一,则认为该国是 大国 :
- 面积至少为 300 万平方公里(即,
3000000 km2),或者
- 人口至少为 2500 万(即
25000000)
编写解决方案找出 大国 的国家名称、人口和面积。
按 任意顺序 返回结果表。
返回结果格式如下例所示。
示例:
输入:
World 表:
+-------------+-----------+---------+------------+--------------+
| name | continent | area | population | gdp |
+-------------+-----------+---------+------------+--------------+
| Afghanistan | Asia | 652230 | 25500100 | 20343000000 |
| Albania | Europe | 28748 | 2831741 | 12960000000 |
| Algeria | Africa | 2381741 | 37100000 | 188681000000 |
| Andorra | Europe | 468 | 78115 | 3712000000 |
| Angola | Africa | 1246700 | 20609294 | 100990000000 |
+-------------+-----------+---------+------------+--------------+
输出:
+-------------+------------+---------+
| name | population | area |
+-------------+------------+---------+
| Afghanistan | 25500100 | 652230 |
| Algeria | 37100000 | 2381741 |
+-------------+------------+---------+
题解:
1
2
3
4
|
# 基础的SQL
# Write your MySQL query statement below
select name, population, area from World
where area >= 3000000 or population >= 25000000;
|
1148 文章浏览I
1148. 文章浏览 I
Views 表:
+---------------+---------+
| Column Name | Type |
+---------------+---------+
| article_id | int |
| author_id | int |
| viewer_id | int |
| view_date | date |
+---------------+---------+
此表可能会存在重复行。(换句话说,在 SQL 中这个表没有主键)
此表的每一行都表示某人在某天浏览了某位作者的某篇文章。
请注意,同一人的 author_id 和 viewer_id 是相同的。
请查询出所有浏览过自己文章的作者
结果按照 id 升序排列。
查询结果的格式如下所示:
示例 1:
输入:
Views 表:
+------------+-----------+-----------+------------+
| article_id | author_id | viewer_id | view_date |
+------------+-----------+-----------+------------+
| 1 | 3 | 5 | 2019-08-01 |
| 1 | 3 | 6 | 2019-08-02 |
| 2 | 7 | 7 | 2019-08-01 |
| 2 | 7 | 6 | 2019-08-02 |
| 4 | 7 | 1 | 2019-07-22 |
| 3 | 4 | 4 | 2019-07-21 |
| 3 | 4 | 4 | 2019-07-21 |
+------------+-----------+-----------+------------+
输出:
+------+
| id |
+------+
| 4 |
| 7 |
+------+
题解:
1
2
3
4
5
6
7
8
9
10
|
# Write your MySQL query statement below
# 使用DISTINCT关键字去重即可
SELECT
DISTINCT author_id AS id
FROM
Views
WHERE
author_id = viewer_id
ORDER BY
author_id ASC
|
































































